このシリーズでは、中高生の皆さんが勉強している数学の知識が、ビジネスの世界でどのように使われているかを紹介します。

数学って、将来必要なの？
と思っている皆さんにぜひ読んでほしいと思います。

■大学受験、決めるなら。

利益の最大化

今回は前々回の記事、数学と仕事#11「利益を最大化する」の続編です。まずは、そのおさらいから。

下記のデータを使って、利益が最大となる販売数量を求めました。

エクセルの機能を使い、販売数量$${(x)}$$と単価$${(U)}$$、および販売数量$${(x)}$$とコスト$${(C)}$$の関係をそれぞれ$${U(x)＝－2.4x＋1600}$$、$${C(x)＝x^2＋20x＋80000}$$と求め、さらにこれらを使い、販売数量$${(x)}$$と利益$${(P)}$$の関係式を下記のように定めました。

この二次関数$${P(x)}$$が最大となる$${x}$$の値が求めたい販売個数となるわけです。結果は$${564}$$個と算出されました。

利益が出る範囲

今回は引き続き、このデータの分析を続けたいと思います。まずは利益が出る販売数量$${(x)}$$の範囲を調べます。下のグラフをご覧ください。

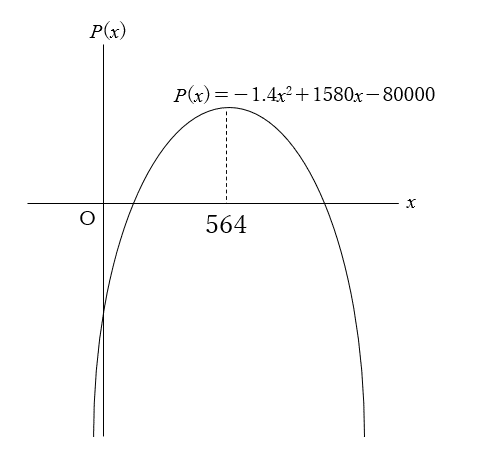
利益が出るのは、$${P(x)}$$＞0の範囲ですから、グラフと$${x}$$軸との交点を調べれば、その範囲を示すことができます。

$${P(x)=-1.4x^2+1580x-80000=0}$$を解く

因数分解は難しいので、解の公式を使いましょう。

$${x=\frac{-1580{\pm\sqrt{1500^2-4･(-1.4)･(-80000)}}}{2･(-1.4)}}$$

ちなみに綺麗な数字にはならなそうです。（現実とはそんなものです。）
実際に計算をしてみたい方は電卓を使ってください。ここでは、途中計算を省略し、結果だけお伝えすると、近似値で$${x＝53, 1075}$$となります。つまり、この商品は販売個数が、$${53＜x＜1075}$$の範囲で利益が出るということが分かったわけです。

商品が持つ稼ぐ力を分析

では、次にこの商品の稼ぐ力について分析してみましょう。もう一度、先のグラフを見てください。利益が出る範囲、$${P(x)＞0}$$の広さに注目です。この範囲（面積）が広ければ広いほど稼ぐ力があると言えるのです。

商品ごとの稼ぐ力を比較したいなら、この面積を調べればいいわけです。ではその方法は？そうです、積分を使えばいいのです。

$${\int_{53}^{1075} (-1.4x^2+1580x-80000) dx}$$

こちらも途中式は省略します。実際の計算には、こちらも電卓が必要ですね。結果は近似値で$${249295574}$$となります。

どうでしょう。数学が現実を把握するための最強ツールであることが実感できたでしょうか。

■大学入試問題に挑戦！中1生の知識で京大数学を解けるかも？！

■人類の未来はユートピアか、それともディストピアか？

■利益を最大化する

■利益と損失の分かれ目は一次関数で分かる

■一次関数で将来予測

■普及率16％のキャズムを越えろ！

■対数ってどう役立つの？

■集合の知識を使ってデータマイニングを学べる！？

■「今すぐに100万円」か、「10年後に130万円」かは数列の和でわかる⁉

■指数関数で読み解く半導体チップの密度とは？

■LINEのリンク数は二次関数的に増加する⁉

■消費者分布のベルカーブは統計を用いる！

■期待収益率は一次関数で説明できる

■Y-SAPIXってなに？

■大学入試情報を無料でお届けします！