
数学と仕事シリーズ#7「魔法のツール~対数」
このシリーズでは、中高生の皆さんが勉強している数学の知識が、ビジネスの世界でどのように使われているかを紹介します。
数学って、将来必要なの?
と思っている皆さんにぜひ読んでほしいと思います。
■大学受験、決めるなら。
かけ算をたし算に、わり算をひき算に変える
対数が考案されたのは1600年代のはじめ、電卓もPCもない時代のことです。大きな数の計算(特にかけ算やわり算)を効率的に行えるよう考え出されました。現在でも対数は重宝されており、有名なところでは地震の規模を表すマグニチュードの計算などに使われています。
大きな数を処理する際、皆さんも知っている下記の公式がその威力を発揮します。なにせ、かけ算をたし算に、わり算をひき算に変換できるのですから(同じケタ数でもかけ算よりはたし算の方が、わり算よりはひき算の方が圧倒的に楽でしょ)。まるで魔法のようです。

では簡単な問題を解いてみましょう。
<問 題>35081×23925を計算せよ
電卓は使わず、常用対数表を使って有効数字3ケタで答えを出してみましょう。以下、底は省略します。(お手元に常用対数表をご用意ください。)
<解 法>
35081≒3.51×$${\gdef\bar#1{#1^4} \bar{10}}$$,23925≒2.39×$${\gdef\bar#1{#1^4} \bar{10}}$$
常用対数表より,log3.51≒0.5453,log2.39≒0.3784
log(3.51×2.39)=log3.51+log2.39≒0.5453+0.3784≒0.9237
ここで常用対数表を使って0.9237の近似値を逆引き。
0.9237≒log8.39
よって,3.51×2.39≒8.39
与式≒3.51×$${\gdef\bar#1{#1^4} \bar{10}}$$×2.39×$${\gdef\bar#1{#1^4} \bar{10}}$$≒839000000
35081×23925を実際に計算すると839312925ですから、いい線いってます。学校で勉強する数学では正確な計算を求められますが、工学など現実の世界では端数は切り捨てますから、これで十分なわけです。
曲線を直線に変える
考案当初は画期的な発見だった対数ですが、現代においてはさすがに上記のような計算をすることはなくなりました。それでも対数の存在意義が薄れたわけではなく、さまざまな領域で活用がなされています。
具体的な例を見てみましょう。
下記の<グラフ①>は2020年2月16日から同年4月11日までの新型コロナウィルスの全国での累計感染者数の推移です。(参照元:厚生労働省ホームページ)。グラフの形から指数関数的な変化が起きていることが分かります。考えればその通りで、1人の感染者が3人にウィルスを拡散すると仮定すると感染者の数は3倍ずつ増えていくわけですから。
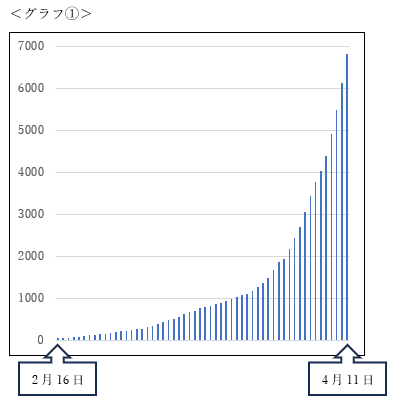
厚生労働省(https://covid19.mhlw.go.jp/extensions/public/index.html)を加工して作成
「データからわかる-新型コロナウイルス感染症情報- 陽性者数(累積)」
2月中の推移には大きな差がないため、変化をとらえるのは難しいですね。そこで縦軸を対数スケールに変換してみましょう。<グラフ①>が曲線$${y=\gdef\bar#1{#1^x} \bar{3}}$$とすると、<グラフ②>はlog $${y=(}$$log$${3)x}$$です。
感染者数の常用対数をとり、グラフを書き換えると下のようになります。
変化の様子を直線的に把握できるようになりました。
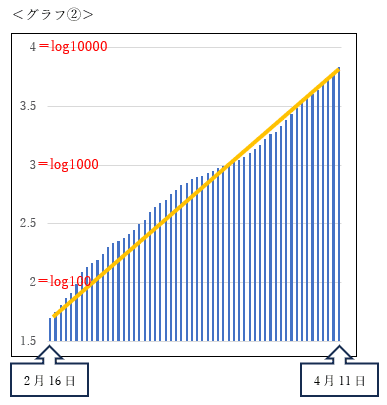
厚生労働省(https://covid19.mhlw.go.jp/extensions/public/index.html)を加工して作成
「データからわかる-新型コロナウイルス感染症情報- 陽性者数(累積)」
いかがでしょうか。今回は対数の紹介でした。
■集合の知識を使ってデータマイニングを学べる!?
■「今すぐに100万円」か、「10年後に130万円」かは数列の和でわかる⁉
■指数関数で読み解く半導体チップの密度とは?
■LINEのリンク数は二次関数的に増加する⁉
■消費者分布のベルカーブは統計を用いる!
■期待収益率は一次関数で説明できる
■Y-SAPIXってなに?

