このシリーズでは、中高生の皆さんが勉強している数学の知識が、ビジネスの世界でどのように使われているかを紹介します。

数学って、将来必要なの？
と思っている皆さんにぜひ読んでほしいと思います。

株式投資のお話

銀行に預けていても、ほとんど利息がつかない時代。
世は投資の話であふれています。

そこで質問です。

あなたの手元に使うあてのない100万円があります。
これをどこかの会社に投資してみよう（つまり株を買うということです）と思います。

どれくらいのリターン（利益）があれば、納得できますか？

ちなみに国の借金である国債は安全性の高い投資です。
なぜなら、国は倒産したりしないからです。

一方、今みなさんが検討している株式投資にはそれなりのリスクがあります。投資した会社の収益が悪化し、配当金がでないとか。
株価は常に流動的ですから、株価が買ったときより大幅に下がるとか。

もっとも最悪のケースが倒産です。そうなれば株券なんてただの紙切れです。鼻紙にもなりません。

リスクを抱えて投資するわけですから、国債と同じリターンでは納得できないわけです。プラス$${α}$$（アルファ）がほしいところです。

投資家が個別株式に対して求めるリターンを期待収益率と言います。
これを理論的に算出する方法があるのです。

それが資本資産価格モデル(CAPM)です。
キャップエムと読みます。（なんかカッコいい）

こちらは1960年代にウィリアム・シャープという経済学者が唱えたものです。彼はこの業績が認められ、1990年にノーベル経済学賞を受賞しています。

期待収益率は一次関数で説明できる

さてここからが数学的な話。

個別株式の期待収益率$${RE}$$を算出する数式は次のようになります。

$${RE＝RF＋β(RM－RF)}$$

(下の図を見ながら、読んでね)
$${RF}$$は無リスク資産の利率で、リスクフリーレートと言います。
実際の算出の際には先に挙げた、国債(10年物)の利率などが用いられます。$${RM}$$は株式市場全体における期待収益率の平均です。

そして、この2つの差$${(RM－RF)}$$をマーケットリスクプレミアムと言います。先ほど述べたプラス$${α}$$の部分です。つまり、リスクをとって投資をするんだから、これくらいの上乗せは欲しいよね、という値のことです。

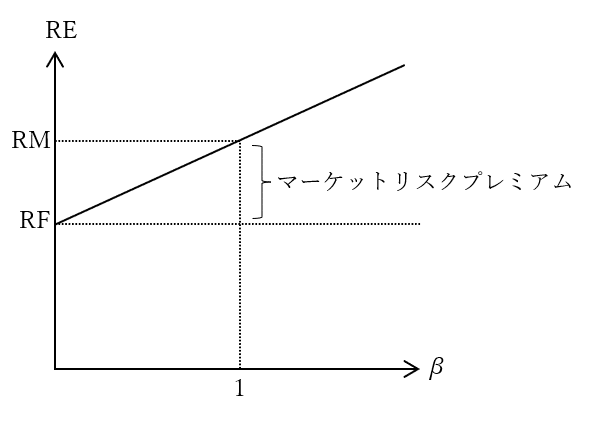
横軸の説明もしておきましょう。
RMが導かれるのは$${β＝1}$$のときです。
$${β}$$とは個別株式が平均的な市場の値動きからどれくらい乖離するかを示す値です。こちらも算出方法が理論化されていますが、今回は説明しません。（興味があれば調べてみてね）

ちなみに$${β＞1}$$であれば平均より値動きが激しいことを、
$${β＜1}$$であれば平均よりも値動きが緩やかであることを、
それぞれ示します。

値動きの大きな会社や業界への投資にはリスクがあり、高いリスクを取るのであれば、相応のリターンが必要であるという前提に立っています。

では実際に計算してみましょう。

某独立行政法人によれば、2020年時点の日本株のマーケットリスクプレミアムは5.6%とのこと。$${RF＝1.0%}$$、$${β＝1.2}$$としてみましょう。数式に代入するだけですね。

$${RE＝1.0＋1.2×5.6＝7.72%}$$

ここからは個人の決断です。年利で7.72%相当のリターンがある株式。
さて、あなたならこれに投資をしますか？

最後にもう一度、上のグラフを眺めてください。

皆さんお気づきの通り、これは中学生が習う一次関数です。

$${x}$$軸に$${β}$$値が、$${y}$$軸に期待収益率がそれぞれ取られているわけです。

直線$${y＝ax＋b}$$の傾き$${a}$$がマーケットリスクプレミアム、切片$${b}$$がリスクフリーレートにあたります。

なんと一次関数でノーベル賞が取れる！
数学には実に夢があります。

■大学受験、決めるなら。