
数学と仕事シリーズ#5「未来のお金の価値」
このシリーズでは、中高生の皆さんが勉強している数学の知識が、ビジネスの世界でどのように使われているかを紹介します。
数学って、将来必要なの?
と思っている皆さんにぜひ読んでほしいと思います。
お金がお金を生む
まずは質問です。
あなたなら次のどちらを選びますか?
(A)今すぐに100万円がもらえる
(B)10年後に130万円がもらえる
答えはどのように前提を置くかで変わってきます。
例えば、年利2%と3%(いずれも複利)の金融商品があったとします。
ちなみに利息の計算方法には単利と複利があります。
単利は元本(もともとあったお金)に対してのみ利息がつきます。
複利は利息を含めた金額に対して利息がつきます。
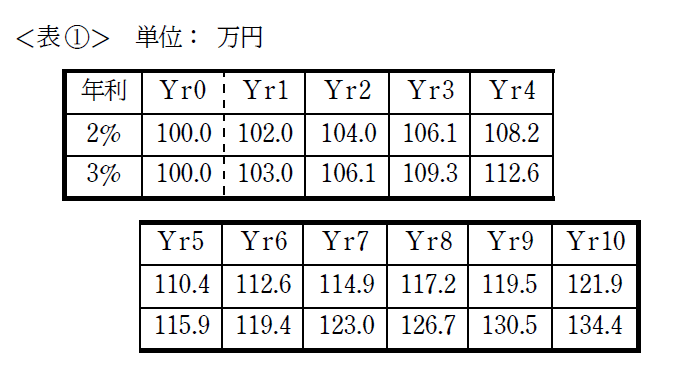
それでは向こう10年の利息を計算してみましょう。
元本は100万円です。
ということで、
✓複利2%の商品を購入できるという前提の場合
「10年後の121.9万円」よりも、「(B)10年後の130万円」のほうがよい
✓複利3%の商品を購入できるという前提の場合
「(B)10年後の130万円」よりも、「(A)今すぐ100万円」をもらって投資に回し、「10年後に134.4万円」としてから回収した方がよい
という答えになります。
個人の資産形成もビジネスも、投資によってお金を増やすことができるという前提に立っています。
ビジネスの話。例えばカフェ。内装工事でお店がいい感じになりました。
それが評判となってお客さんがたくさん来るようになりました。「投資→増収」のサイクルが生まれたわけです。
お金がお金を生む。
成長率を3%とした場合、現在の100万円と10年後の134.4万円は同じ価値を持っていると考えます。(<表①>を見てね)
現在価値を計算する
では次の質問です。成長率は、変わらず3%とします。
あなたはあるソフトウェアを開発することを考えています。開発費用として380万円がかかる見込みです。利益としては発売の翌年から4年間、毎年100万円の利益を見込んでいます。さてこの投資、実行すべきですか?
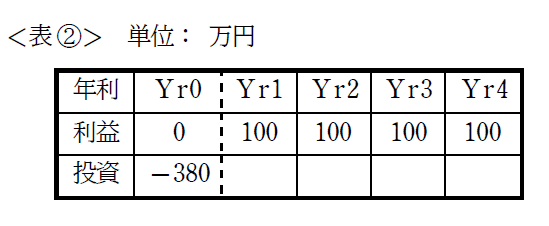
4年間の利益の合計が400万円になるので、開発費用380万円を上回っており、投資効果ありと判断するのは早計です。
なぜなら、未来の100万円は現在の100万円ではないからです。
<表①>をもう一度見てください。

もし3%ずつお金が成長するとしたら、4年後に100万円は112.6万円に増えているはずです。
では4年後の100万円は現在の価値に換算したらいくらなのでしょうか?
簡単ですね。100÷$${\gdef\bar#1{#1^4} \bar{(1.02)}}$$です。
このように前提となる成長率で未来のお金を割り戻し、現在価値(PV=Present Value)を算出する考え方があります。
この方式をDCF法(Discount Cash Flow)と言います。
これを数式に表すと以下のようになります。

ここでは利息を使って説明しましたが、実際の計算では、割引率には資本コストを用います。(資本コストについてはここでは説明をしません。興味のある人は調べてみてね。)
では改めて<表②>の内容を精査してみましょう。

上記の数式を使ってPVを計算すると、371.7万円となります。
投資額である380万円をわずかに回収できません。
もし複利3%の金融商品を購入できるなら、そちらの方が儲かるということですね。
お金は賢く増やすものなのです。
■大学受験、決めるなら。

