このシリーズでは、中高生の皆さんが勉強している数学の知識が、ビジネスの世界でどのように使われているかを紹介します。

数学って、将来必要なの？
と思っている皆さんにぜひ読んでほしいと思います。

■大学受験、決めるなら。

恐怖の関数

$${y=\dfrac{a}{2040-x}}$$

上記の数式はChatGPTを開発した米オープンAIの元幹部イリア・サツキバー氏が提唱したものです。この関数はどのようなグラフを描くでしょうか。数Ⅲで学習する分数関数ですが、複雑な式ではないので、数学が得意な皆さんなら想像ができるのではないでしょうか。そうです。中学1年生で習う反比例のグラフをx軸方向に平行移動させたものになります。

aは比例定数、xは年数（西暦）、yは国民総生産(GNP)を表します。サツキバー氏はどの国にもこの法則が当てはまるとしています。トロント大学のジェフリー・ヒントン名誉教授はこの数式を「とても恐ろしい関数」と評しました。どういうことでしょう？

GNPの爆発的な成長

まずはグラフを描いてみましょう。

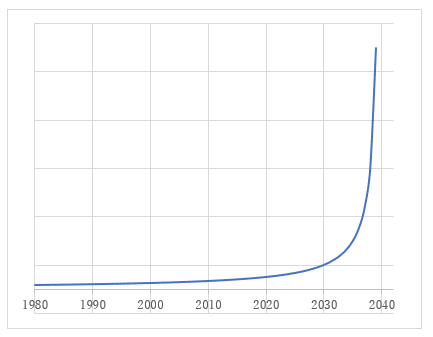
このグラフから人類の歴史と未来を読み解いてみましょう。

人類の歴史にはいくつかの転換点がありました。最初のそれは1万2千年前に起きた農耕社会の広まりです。その後、18世紀に始まった農業革命を経て、20世紀の情報革命へと続きます。こうした社会の大変革を経ても、GNPの成長は緩やかなものでした。

もう一度、グラフを眺めてみてください。もうすぐGNPの爆発的な成長が起こります。2040年にはその値は無限大に達します。サツキバー氏は、その原動力になるのがAIであるとしています。

人類の未来はユートピアか、それともディストピアか？

GNPの成長はどの国にとっても喜ばしいことです。では、なぜこれが恐怖の関数なのでしょうか。ヒントン氏は、AIが成長を遂げ、無限ともいえる生産性を達成する未来では、人間の存在が無価値になると考えたのです。

あなたはAIの活用が進んだ人類の未来がバラ色のユートピアになると思いますか？　それとも暗黒のディストピアになると思いますか？

数学は、こんなことを考えるきっかけにもなるのですね。

#最近の学び

■大学入試問題に挑戦！新中1生の知識で京大数学を解けるかも？！

■利益を最大化する

■利益と損失の分かれ目は一次関数で分かる

■一次関数で将来予測

■普及率16％のキャズムを越えろ！

■対数ってどう役立つの？

■集合の知識を使ってデータマイニングを学べる！？

■「今すぐに100万円」か、「10年後に130万円」かは数列の和でわかる⁉

■指数関数で読み解く半導体チップの密度とは？

■LINEのリンク数は二次関数的に増加する⁉

■消費者分布のベルカーブは統計を用いる！

■期待収益率は一次関数で説明できる

■Y-SAPIXってなに？

■大学入試情報を無料でお届けします！