このシリーズでは、中高生の皆さんが勉強している数学の知識が、ビジネスの世界でどのように使われているかを紹介します。

数学って、将来必要なの？
と思っている皆さんにぜひ読んでほしいと思います。

■大学受験、決めるなら。

一次関数で将来予測

皆さんは回帰分析という言葉を聞いたことがありますか。
数Ⅰ「データの分析」で、散布図と相関について学びましたね。その延長線にあるのが回帰分析です。すなわち、回帰分析とは目的変数と説明変数の間にどのような関係が成り立つかを調べる方法です。2つの変数の関係は一次関数で表現します。（これを回帰式といいます。一次関数であることがポイント）

ビジネスにおいてはこれを将来予測に使います。
例えば、広告費（説明変数）と売上（目的変数）の間に正の相関があり、それを回帰式(y＝ax＋b)で表すことができれば、広告費を増やしたときにどれだけ売上が伸びるかを予測できます。

ちなみに回帰式はエクセルなどを使えば一瞬で計算できます。（興味のある人は試してみてね）

単回帰分析と重回帰分析

先ほど広告費と売上を例にとりましたが、現実にある事象はそう単純なものではありません。物事の因果関係というのは複雑に絡み合っているものです。再び売上を例にとるならば、広告費以外にも(小売業なら)店舗数とか店舗面積や商品点数、従業員数なども影響しそうです。また数値化することが難しい店舗の立地や従業員の接客スキルなども重要な因子になるでしょう。

こうした複雑な状況を説明する手法はないものか？

（数値化できないものはちょっと置いておくとして）目的変数と複数の説明変数の関係を分析する手法が重回帰分析です。ちなみに目的変数と説明変数が１対１で対応しているのが単回帰分析です。重回帰分析の回帰式は以下のようになります。

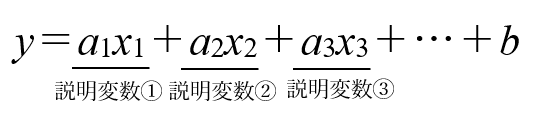
こちらもエクセルなどを使えば簡単に導くことができます。数学で未来を予測する。大事な発想です。

■普及率16％のキャズムを越えろ！

■対数ってどう役立つの？

■集合の知識を使ってデータマイニングを学べる！？

■「今すぐに100万円」か、「10年後に130万円」かは数列の和でわかる⁉

■指数関数で読み解く半導体チップの密度とは？

■LINEのリンク数は二次関数的に増加する⁉

■消費者分布のベルカーブは統計を用いる！

■期待収益率は一次関数で説明できる

■Y-SAPIXってなに？

■大学入試情報を無料でお届けします！