
数学と仕事シリーズ#11/利益を最大化する
このシリーズでは、中高生の皆さんが勉強している数学の知識が、ビジネスの世界でどのように使われているかを紹介します。
数学って、将来必要なの?
と思っている皆さんにぜひ読んでほしいと思います。
■大学受験、決めるなら。
関数を使って状況を可視化する
皆さん、次の式は大丈夫ですね。
利益=売上-コスト
利益を最大化したい。誰しもがそう思います。では売上を伸ばしさえすればいいのでしょうか。そうはならないのが、ビジネスの難しいところです。なぜなら、コストの増減が売上の増減と一致しないからです。今日は実例を使いながら、利益が最大になるポイントをどのように探すか、考えてみましょう。
では、まず元になるデータを確認してください。

ある会社の1月から8月までの販売データです。それぞれの月の販売数量、単価(1個あたりいくらで売ったか)、かかったコストを一覧にしたものです。
この表を眺めていても、どこに利益が最大化するポイントがあるのか、さっぱり分かりません。そこで、まずは関数を使って状況を把握してみましょう。
エクセルをフル活用する(1)
エクセルには2つの変数の間の関係式を求める機能があります。それを使って、まず販売数量$${(x)}$$と単価$${(U)}$$との関係式を調べます。(エクセルの操作方法について、割愛します。興味のある人はググってみてね)
すると次のようなグラフと関係式が得られました。

$${R^2}$$の値はデータが得られた関係式とどの程度近似しているかを示しています。$${R^2=1}$$はデータと関係式が完全一致した状態です。上のグラフの0.997はかなり高い数値です。確かに点がほぼ一直線に並んでいます。
エクセルが求められるのは一次関数だけではありません。当然、データは一定の割合で変化するとは限らず、増減することもあります。指定をすれば、二次関数、三次関数などの式を求めることもできます。試しに同じデータを二次関数で表現したら、どうなるか試してみましょう。
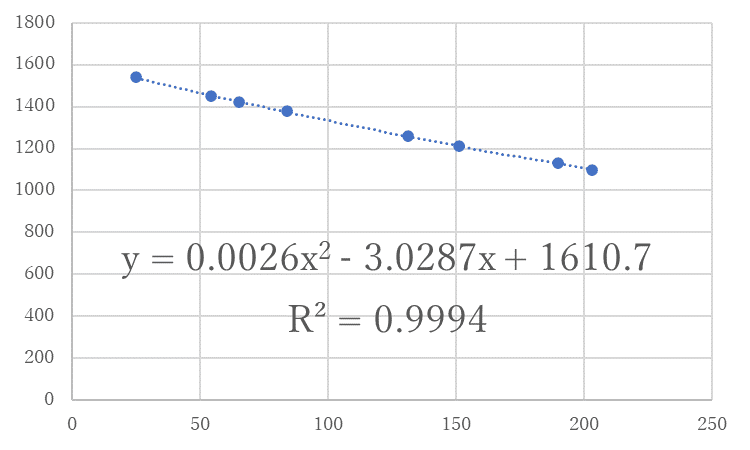
なんと、先ほどよりも$${R^2}$$の値が高くなっています。二次関数の方がより状況を正しく表現できるということです。ただし、この後の計算を楽にするために、ここでは一次関数の関係式を採用することにしましょう。さらに係数の有効数字を2ケタにまるめ、$${U(x)=-2.4x+1600}$$とします。(ビジネスでは経済簡便性という考えも重要なのです!)
エクセルをフル活用する(2)
では、次は販売数量$${(x)}$$とコスト$${(C)}$$の関係式を調べてみましょう。まずは一次関数で表現してみます。

0.9672は決して低い数値ではありませんが、点のバラつきが少々気になります。では二次関数を使ったらどうなるでしょうか。

見事に$${R^2=1}$$となりました。今度はこちら二次関数の関係式を採用します。こちらも係数の有効数字を2ケタとし、$${C(x)=x^2+20x+80000}$$とします。
利益が最大化する販売数量は?
いよいよ、つくった2式を使って、利益が最大化する販売数量を求めます。次のように考えればいいですね。
$${P(x)=x・U(x)-C(x)}$$ ※利益=単価×販売個数-コスト
$${P(x)=x(-2.4x+1600)-(x^2+20x+80000)}$$
$${=-1.4x+1580x-80000}$$
ちなみに$${U(x)}$$を一次式としたのは$${P(x)}$$を二次関数にするためでした。
あとは頂点の座標を求めるだけです。平方完成の計算はちょっと大変そうなので、微分を使いましょう。
$${P’(x)=-2.8x+1580=0}$$
よって、$${x≒564}$$
この値を超えて販売した場合、利益が低下していきます。ある点から先は、利益が出なくなります。(では、そのある点とは販売個数が何個のときでしょう? 皆さん、考えてみてください。)
データを眺めていただけでは分からない、こうした現象を数学が可視化してくれるのです。
■大学入試問題に挑戦!新中1生の知識で京大数学を解けるかも?!
■利益と損失の分かれ目は一次関数で分かる
■一次関数で将来予測
■普及率16%のキャズムを越えろ!
■対数ってどう役立つの?
■集合の知識を使ってデータマイニングを学べる!?
■「今すぐに100万円」か、「10年後に130万円」かは数列の和でわかる⁉
■指数関数で読み解く半導体チップの密度とは?
■LINEのリンク数は二次関数的に増加する⁉
■消費者分布のベルカーブは統計を用いる!
■期待収益率は一次関数で説明できる
■Y-SAPIXってなに?
■大学入試情報を無料でお届けします!


