皆さん、こんにちは。高校数学で現実世界を切り込む「実社会シリーズ」が第3弾を迎えました。前回の記事(#18)では「地図×三角比」を扱いましたが、今回は「通信×整数」と題して、RSA暗号の仕組みを見てみましょう。

〇暗号と素数

「通信では素数を使って暗号化する」「素因数分解の大変さがカギになる」ということを知っている人も多いと思います。なんとなく難しそう…と思いがちですが、実は高校で習う「整数」の知識だけで理解できる仕組みを使っています。「通信社会を支える」という数学の一面を眺めてみましょう！

■高校数学をより深く使い、「一歩先の数学」の世界へ！

〇文字から数字へ

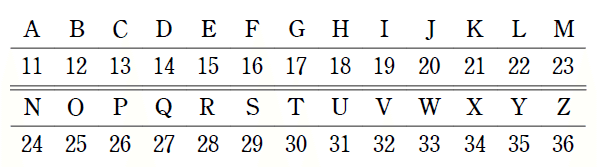
暗号を支えるコンピュータは、文字よりも数字の方が得意です。試しに上の対応表を使って「SAPIX」を数字列に直してみると、「2911261934」になります。一方、「2911261934」と上の対応表があれば「SAPIX」をすぐに復元できるので、数字列に直しただけでは、残念ながら暗号とは言えません。うまくシャッフルすることが必要なのです。

〇ナンバーキーを回そう

さて、ここからは想像力を高めてください。あなたは「$${p，q}$$」という、誰にも見せない「異なる素数の鍵」を持っています。一方、全世界に公開されているのは、「$${pq，k}$$」を使う、「メールソフトpqk」です。人々は、このメールソフトを使って、あなたにメッセージを送ります。ちなみに、この$${k}$$は「『1以上$${pq}$$以下で、$${pq}$$と互いに素な自然数の個数』と互いに素な自然数のひとつ」です。(少しややこしいですね)

具体例で考えましょう。例えば、あなたが持っている鍵が「$${p=3，q=7}$$」なら、$${pq=21}$$です。1以上21以下で、21と互いに素な自然数を数えてみれば12個なので、例えば「$${k=5}$$」などが該当します。以下は、「$${pq=21，k=5}$$」を使う「メールソフト215」で考えましょう。

さて、誰かがあなたに「JAPAN」というメッセージを送るとします。相手が入力した「JAPAN」は、冒頭の対応表を使って「2011261124」に直されます。そして、この数字列は「$${pq}$$桁ごと」を目安に区切られます。いまは$${pq=21}$$なので、メールソフト215は「20桁ごと」に区切ります。今回の数字列は短いので、「2011261124」のまま使われます。続いて、メールソフトはこの数字を次のルールで加工します。

今回は「$${X=2011261124，k=5，pq=21}$$」なので$${\gdef\bar#1{#1^5} \bar{2011261124}}$$を21で割った余りを求めることで、加工後の数字は「17」です。あなたが使うメールソフト215は「17」を受信し、「解読」の手続きに入ります。メールソフト215は次に述べる【問題2】を瞬時に解き、冒頭の対応表でアルファベットに直し、あなたは「JAPAN」というメッセージを無事入手します。

■SAPIXメソッドを活かした大学受験塾！Y-SAPIXって知ってる？

〇盗み見られてしまったら？

相手とあなたを繋ぐ回線を流れているのは「17」なので、メッセージを盗み見た人の手元にあるのは「メールソフト215を使っている」「メッセージは17」という2つの情報だけです。盗み見た人がメッセージを解読するには、次の【問題1】を解く必要があります。

一方、あなたのメールソフトが解くのは、【問題2】です。

2つの違いは「ただし、21=3×7」の有無だけですが、素数鍵「$${p，q}$$」がもっと大きな桁数になると、【問題1】は【問題2】に比べて遥かに多い計算を必要とし、事実上の「解けない問題」と化します。

つまり、「受信者」は簡単に読めて、「傍受者」は読めないという通信のセキュリティが実現するのです！ 「$${p}$$と$${q}$$が分かれば簡単に解けること」の説明は省略しますが、「ユークリッドの互除法」「1次不定方程式」「合同式」という、高校数学で習う事柄を押さえていれば理解できます。興味のある方は、ぜひ調べてみてください。

それでは、次の「実社会シリーズ」で再びお会いしましょう！

■大学受験、選ぶなら。

■大学入試情報を無料でお届けします！

■数学こぼれ話#18　実社会シリーズvol.2　～地図を見るにも三角比～

■数学こぼれ話#16　実社会シリーズvol.1　～二次関数で野球を考えよう～

■対話シリーズを含む「数学こぼれ話」過去の記事はこちら

■入試問題分析・解法に関する記事はこちら

■Y-SAPIXで数学を始めよう！