皆さん、こんにちは。
2023年度の数学こぼれ話は「対話シリーズ」と「実社会シリーズ」の2本柱で進んでいきます。

実社会シリーズは、「高校数学を使って身近な物事を考察してみよう」というシリーズです。共通テスト対策にも是非！

さて、先日のWBCでは3大会ぶり3回目の日本優勝に、国内が大いに沸き上がりました。

そこで、今回のテーマは野球×二次関数とし、「高校数学」という観点から野球に斬り込んでみましょう。

〇単純な「モデル」を作ろう

現実世界で起こる現象は、様々な要因が複雑に絡み合っています。
もちろん、今回のテーマである「野球」も例外ではありません。

フィールドの気温・風・空気抵抗、選手たちの戦略・読み合い・選手ごとの特性…。これらを全て考慮しようものなら、もはやコンピュータの仕事です。

ここでは、手計算で扱えるように単純化した「モデル」を作りながら、考えてみましょう。まず、バッター・ショート・レフトの位置と特性は、下図のようにします。

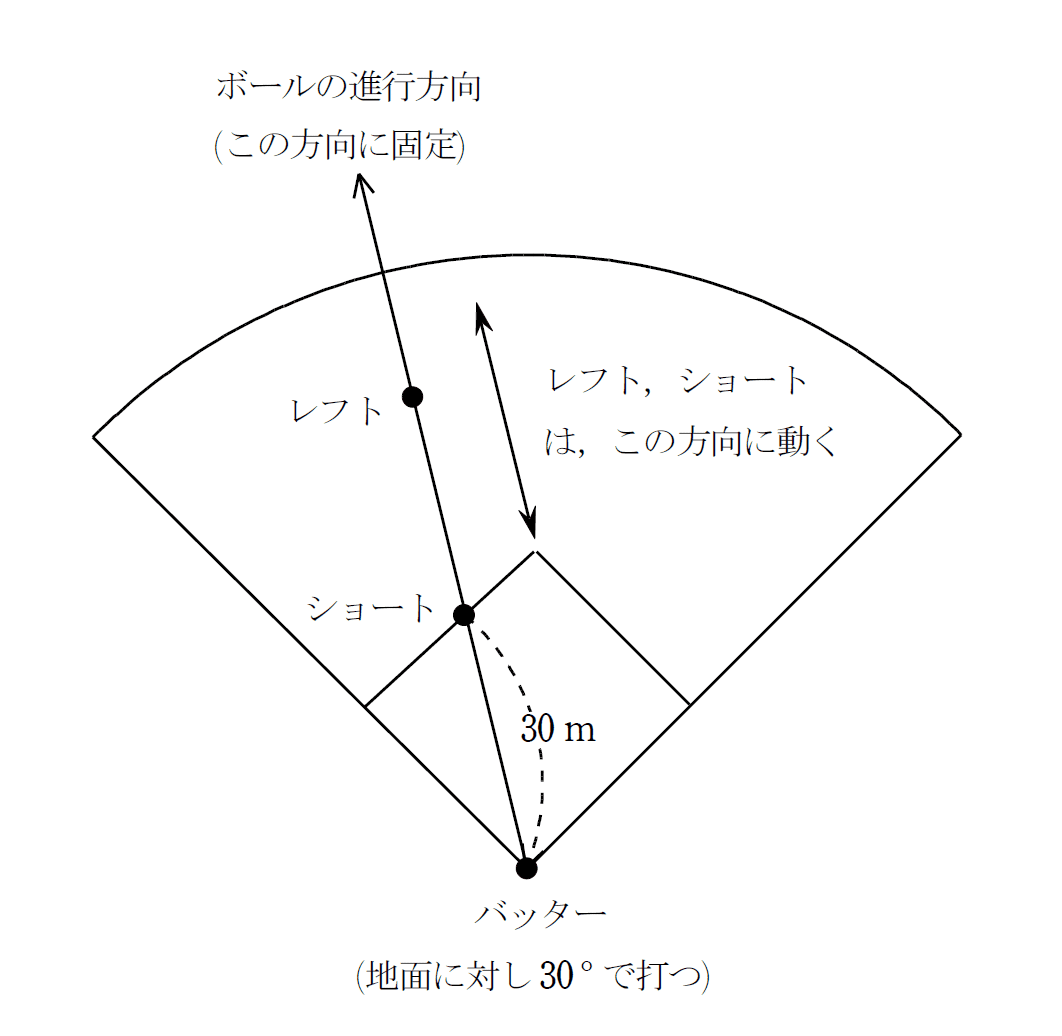
役割の確認をしておくと、「ショート」は塁付近の守備をし、「レフト」は外野の守備をします。また、ボールの動きに影響を与える風や空気抵抗は全くないものとし、人やボールの大きさも無視します。

〇ボールの軌道は放物線を描く！

バッターが打ったボールの速さ(打速)を$${𝑣[m/s]}$$とすると、ボールの軌道は放物線を描きます。二次関数のグラフですね。バッターを原点O、ボールの進行方向を$${x}$$軸、地面からの高さ方向を$${y}$$軸にとれば、この放物線を表すおよその式は

$${y=-\dfrac{20}{\gdef\bar#1{#1^2} \bar{3v}}\gdef\bar#1{#1^2} \bar{x}＋\dfrac{1}{\sqrt{\smash[b]{3}}}x\cdots(*)}$$

と書けます。(※詳しい計算は省略します。)$${𝑣[m/s]}$$が大きいほど放物線は平べったく、最高到達点は高くなることが分かります。下の図も参考にしてみてください。

〇ショートか？ レフトか？

$${(＊)}$$を見ると、ボールの軌道は打速$${𝑣[m/s]}$$だけで決まることが分かります。バッターから$${30m}$$に待機しているショートの所にボールが落ちてくるのは、どのような打速のときでしょうか？　放物線が再び$${x}$$軸と交わるときを考えれば、次のように計算できますね。

$${(＊)}$$で$${y=0}$$として

$${0=-\dfrac{20}{\gdef\bar#1{#1^2} \bar{3v}}\gdef\bar#1{#1^2} \bar{x}＋\dfrac{1}{\sqrt{\smash[b]{3}}}x}$$

$${x≠0}$$として$${x=\dfrac{\sqrt{\smash[b]{3}}}{20}\gdef\bar#1{#1^2} \bar{v}}$$なので、$${x=30}$$となるのは$${\dfrac{\sqrt{\smash[b]{3}}}{20}\gdef\bar#1{#1^2} \bar{v}=30}$$より

$${v=\sqrt{\smash[b]{200\sqrt{\smash[b]{3}}}}≒19[m/s]}$$

のとき。

$${19[m/s]}$$といえば時速$${68km}$$ 程度です。打速の平均は少年野球でも時速$${70～100km}$$ と言われているので、ショートの所にボールが落ちてくることはほとんど無く、大体は背後の方に飛んでいきますね。したがって、動ける範囲が広いショートほど「遊撃手」としてレフトに頼らずボールを捕り、より確実に塁を守ることができるというわけです。

ところで、上の計算で「落下地点を与える式」として出てきている

$${x=\dfrac{\sqrt{\smash[b]{3}}}{20}\gdef\bar#1{#1^2} \bar{v}}$$

もまた、打速$${𝑣[m/s]}$$の二次関数なので、$${𝑥}$$はすぐに大きな値をとることにも注意しましょう。
例えば、$${𝑣}$$が$${30[m/s]}$$のときは$${𝑥 ≒ 78[m]}$$なので、ここまで来たらボールを捕るのはレフトに任せ、ショートは「中継」という役回りに切り替えるのがよいでしょう。

もちろん、実際のプレーは上の考察よりも遥かに複雑です。数式を使って計算こそしないものの、選手たちは様々なプレーや試合を通じて「データベース」を作り上げ、その場その場で最適な判断を下しながら動いているのですね！

それでは、次の「実社会シリーズ」で再びお会いしましょう！

■Y-SAPIXで数学を始めよう！