皆さん、こんにちは。高校数学で現実世界を切り込む「実社会シリーズ」が第4弾を迎えました。今回は高校数学の道具を総動員し、パラボラアンテナの仕組みを理解してみましょう。

〇車窓から外を眺めてみよう

高架の上を走る電車に乗っているとき、1m弱くらいの大きさをした「平べったい器」が建物の屋根に付いているのを見たことはありますか？ 「パラボラアンテナ」と呼ばれており、テレビ用の電波をキャッチするために設置されている装置だと知っている人も多いと思います。正式名称をparabolic antennaと言い、”parabolic”は「放物線状の」という意味の形容詞です。どうやら、「放物線」がカギになっていそうです。この記事では高校数学の知識を駆使しながら、パラボラアンテナの仕組みを解き明かすことを目指します！

■SAPIXメソッドを活かした大学受験塾！Y-SAPIXって知ってる？

〇モデル化しよう

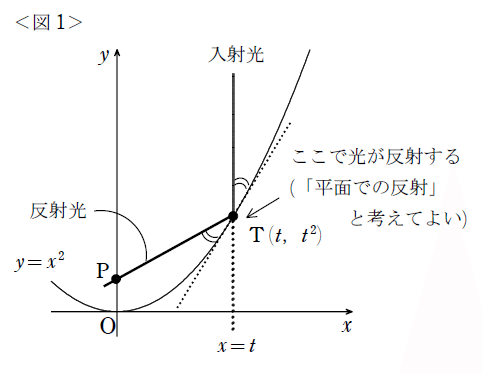
パラボラアンテナは、皆さんがよく知っている「放物線」を軸まわりに1回転させて作られる形状で、数学では「放物面」と呼ばれています。この放物面に対して、無数の電波が平行に差し込んでいるのです。しかし回転させれば同じことなので、＜図1＞のような図を考えれば十分です。

■高校数学をより深く使い、「一歩先の数学」の世界へ！

〇反射光の行く先は？

反射光が$${y}$$軸と交わる点Pは、$${t}$$(>0)の値に依存するのでしょうか？ ここからは様々な単元内容のオンパレードですが、頑張ってついてきてください。さて、Pの座標を求めるには、反射光、つまり直線PTの式が求まればOKです。そして、この直線PTはT$${(𝑡，\gdef\bar#1{#1^2} \bar{t})}$$を通ることが分かっているので、結局は直線PTの傾きが求まれば解決です。(このような「逆算思考」は、問題を解く上で大切です。)

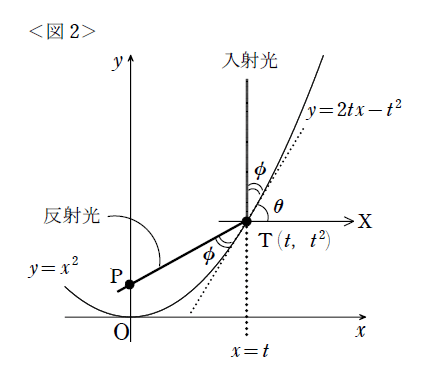
＜図2＞のように$${\theta}$$を定めると、$${tan(\dfrac{π}{2}－θ)}$$の値はTでの接線の傾き$${2t}$$に等しいので、$${tan(\dfrac{π}{2}－θ)＝2t}$$、つまり$${tanθ=\dfrac{1}{2t}}$$が成り立ちます。そして、XTからPTまで測った角は$${\dfrac{3}{2}π－2θ}$$と表されるので、直線PTの傾きは$${tan(\dfrac{3}{2}π－2θ)=t－\dfrac{1}{4t}}$$と求まります。よって、直線PTの式はとうとう$${y=(t-\dfrac{1}{4t})x＋\dfrac{1}{4}}$$…(＊)と求まります。(※このあたりの計算は結構大変です。三角関数に自信のある方は、ぜひ自分で途中計算を追ってみましょう。)

■大学受験、選ぶなら。

〇結果を吟味しよう

反射光の式(＊)は、「どのような$${𝑡}$$(>0)に対しても$${𝑦}$$切片が$${\dfrac{1}{4}}$$である」という、極めて大きな特徴を持っています。
つまり、放物線の上で反射した光は、必ず点P$${(0，\dfrac{1}{4})}$$を通ることが分かります。よって、この部分にアンテナの受信機を取り付けておけば、あらゆる入射光(電波)を漏れなく1 点でキャッチできるのです！ 放物線が持つこのような性質を最大限に活かして作られたのが、街中で見かけるパラボラアンテナというわけですね。

それでは、次の「実社会シリーズ」で再びお会いしましょう！

■大学入試情報を無料でお届けします！

■実社会シリーズを含む「数学こぼれ話」過去の記事はこちら

■共通テスト対策にも役立つ！過去の対話シリーズはこちら

■入試問題分析・解法に関する記事はこちら

■Y-SAPIXで数学を始めよう！