皆さん、こんにちは。Y-SAPIX数学科がお届けする対話シリーズ、第2弾のテーマは「虚数単位$${i}$$」です。多くの高校生を悩ませてきた「見えない数」を、色々な角度から眺めてみましょう！

Y太とS子は高校2年生。数学IIの教科書で「虚数単位$${i}$$」を予習してみたものの、すっかり混乱中…。

Y太：2乗して－1になる数…。いかにも「目に見えない数」という感じでモヤモヤするなぁ。計算自体は大して難しくないけど、とにかく実体が無さすぎて…。
S子：「急に降って湧いた感」がすごいよね。
Y太：数の範囲を「実数→複素数」と拡張しているから、難しいのは当たり前なのかもしれないね。√が初めて出てきたときも、結構苦労したからなぁ。
S子：数の範囲を拡張すると「何かが便利になる」という感覚があるかな。例えば「整数」の範囲では＋－×は考えられるけど、÷が考えられなかったりするし。3÷4は整数にならないからね。でも、数の範囲を「有理数」まで拡張すれば、＋－×÷の全てを考えられるようになる！
Y太：そういえば、そもそも「数」って目に見えないよね。散歩していたら今日は道端で「2」を見つけました、とはならないし。どのみち何も見えないんだし、「便利な枠組み」ならどんどん受け入れた方がいい気がしてきた。
S子：2個の石、2本の木、…。たまたま私たちが「自然数が投影されやすい世界」に暮らしているから、自然数を分かりやすいと思うだけなんだろうね。もしかしたら、虚数でさえ「当たり前」と感じられる世界がどこかにあるのかも？
Y太：だんだんと哲学的な話になってきた…。ところで、虚数単位$${i}$$を受け入れると、「重解も区別すれば、2次方程式はちょうど2個の解をもつ」みたいな、歯切れの良い主張をできるようになるね。図1と図2を比べてみよう。

S子：推測だけど、一般的に「重解を区別すれば、$${n}$$次方程式はちょうど$${n}$$個の解をもつ」ということも言えそう。2次方程式なら2個、3次方程式なら3個、…。簡単にイレギュラーが発生してしまう数学よりも、一般的な主張が色々と成り立つ数学の方が、統一感があって良いね。

Y太：「実感」という意味では、図を使ってみるのも良いかもしれないな。実数と点を対応させるには「数直線」を使うので、複素数なら…。
S子：(実数)+(実数)$${i}$$なので、「平面」が良いんじゃないかな。例えば、2なら点(2，0)、3$${i}$$なら点(0，3)、1+2$${i}$$なら点(1，2)を対応させていく感じで。これを使うと、「複素数の計算」と「点の動き」は、図3のように対応しているね。

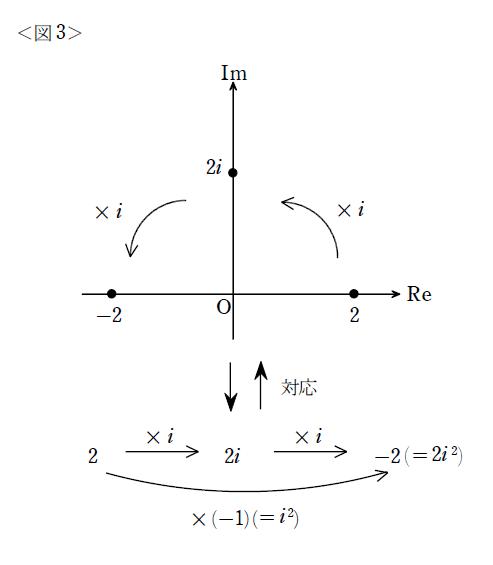
Y太：要するに、複素数をかけると「伸び縮みと回転」が同時に起こるんだなぁ。実際に点を回すために使うと、けっこう実感を持てて良いね。しかも、「マイナス×マイナスがプラス」というのも、すごく当たり前。
S子：「マイナス×マイナスがプラス」は、私も「裏の裏は表！」みたいに無理やり理解してたなぁ。こうして見てみると、色々な事柄がすっきり分かりやすくなるね。謎だらけだった虚数単位$${i}$$への好感度が、だいぶ上がってきたかも！
Y太：良い意味で調子に乗ってきたところで、もう少し予習を進めてみようか！

ちなみに、S子の発言にある「虚数を当たり前に感じられる世界」として、量子力学によって記述される「ミクロな世界」が挙げられます。力学での「運動方程式」にあたる基本方程式の中には、当然のように虚数単位$${i}$$が入っているのです。また、「複素数で考えると、$${n}$$次方程式はちょうど$${n}$$ 個の解をもつ」というS子の推測は正しく、これは「代数学の基本定理」と呼ばれています。どちらも高校範囲を少し超えた内容ですが、興味のある方はぜひ調べてみてください。

それでは、次の「対話シリーズ」で再びお会いしましょう！

■過去の記事はこちら

■入試問題分析・解法に関する記事はこちら

■Y-SAPIXで数学を始めよう！