
数学こぼれ話#29 ~データを直線で近似してみよう~
皆さん、こんにちは。身のまわりには、「高校数学」の力を借りると一歩深く理解できる事柄で満ちています。今回は「データの近似」と称して、最小二乗法の仕組みについて見ていきたいと思います。統計に関係する用語を少し使いますので、知識に不安のある方はこちらの記事もどうぞ。(数学こぼれ話#10 ~相関係数を徹底理解~)
〇似ている直線を引こう
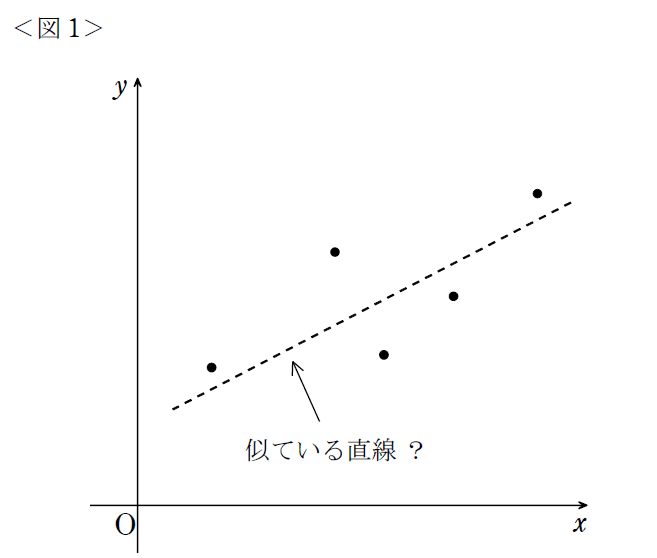
理科の実験などで、いくつかプロットした点をもとに「直線を1本引きましょう」と言われたことはありますか? あるいは、Excelなどを使って「似ている直線」を描いたかもしれません。<図1>も見てみてください。点線で示した直線は、確かに5個の点から「自然」に引ける線と言えそうですが、「これで一番正確か?」と言われると疑問が残ります。Excelなどで描いた直線であれば一番正確でしょうが、すると今度は「どのようにして直線は決まっているのか?」という疑問が出てきます。
〇最小二乗法のしくみ
近似直線を求めるポピュラーな方法に、「最小二乗法」というものがあります。Excelでは、”=LINEST”という関数を使うと一発で引くことができます。「直線を決定すること」は「傾き$${a}$$と切片$${b}$$を決定すること」と同じですが、最小二乗法では次のような発想で、傾き$${a}$$と切片$${b}$$を求めます。<図2>をご覧ください。
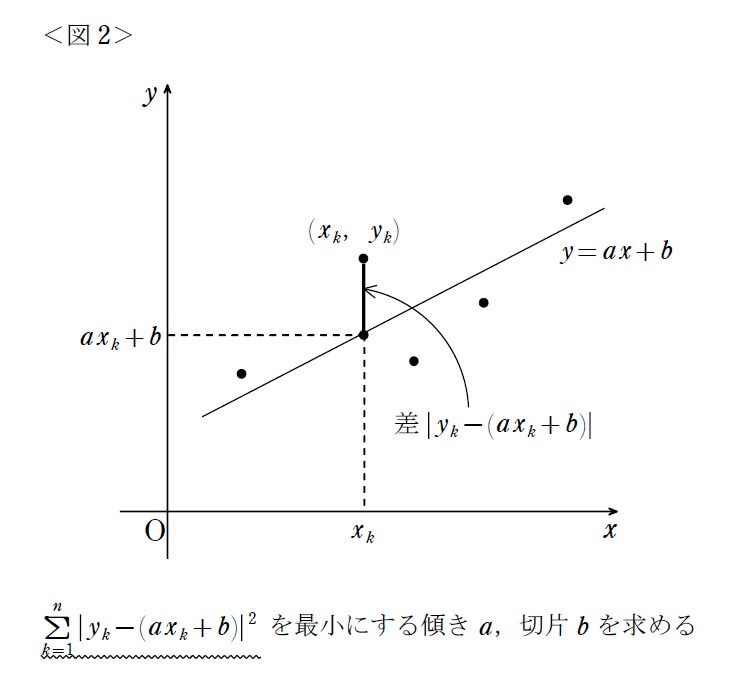
波線で示したのは、「$${n}$$個分の誤差を集めたもの」と考えてもらえばOKです。波線の値が小さければ小さいほど、$${n}$$個のデータを上手く直線$${y=ax+b}$$で近似できた、と言ってよさそうですね。では、$${a}$$と$${b}$$の求め方を眺めてみましょう。展開すれば2次式なので、(かなり気合を入れれば)実際に計算することもできます。
〇計算してみよう
展開して整理すると、次のような式が得られます。

思わず「…」となってしまう式ですね。しかし、$${a^2}$$と$${b^2}$$の係数が共に正の2次式なので、「平方完成して2乗を作る」という基本手順を踏んでいけば、(*)が最小になるような組$${(a, b)}$$を求められます。計算は省略しますが、最終的に次のような「公式」が得られます。

Excelであれば、平均は”=AVERAGE”、分散は”=VAR”、共分散は”=COVARIANCE”で求まりますので、具体的に色々と計算してみると面白いかもしれません。
それでは、次の「こぼれ話」でお会いしましょう!
■大学入試情報を無料でお届けします!

■大学受験の総合情報サイト→ぜひホーム画面に追加してご確認ください!
■対話シリーズを含む「数学こぼれ話」過去の記事はこちら
■入試問題分析・解法に関する記事はこちら

