皆さん、こんにちは。
Y-SAPIX数学科がお届けするこぼれ話では、高校数学を少し深く眺める＆楽しむためのヒントをお伝えしていきます。

前回(数学こぼれ話#33　～「有名な置換積分」に隠された秘密～)に続き、今回も数学Ⅲの積分法をテーマに、「置換積分」を感覚的に理解することを目指します。

〇計算の確認

$${\int_{0}^{4}𝑓(𝑥)𝑑𝑥}$$という定積分を計算するときに、$${x=t^2}$$(ただし$${𝑡≧0}$$)という置き換えをすると、次のような書き換えが起こるのでした。

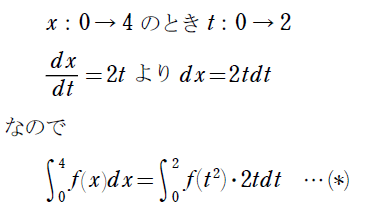
「ルール」と割り切ってしまえば単純で、かつ証明を追えば(*)が正しいことは分かるのですが、(*)を「当たり前」と思いたくなってきます。どう考えたらよいでしょうか？

〇図形的に考える

現在の高校数学では積分を「微分の逆操作」で教えることが主流になっています。これはもちろん正しいのですが、「定積分を使って面積を計算できる」という事実と結び付きづらい、という難点があります。

少し前の記事(数学こぼれ話#14　お役立ちシリーズvol.7～定積分の「意味」を知ろう～)では「定積分＝符号付き面積」ということを強調しました。

ざっくり言うと、符号付き面積というのは「$${x}$$軸の上側ならプラス、$${x}$$軸の下側ならマイナス」とする、面積を拡張した概念です。$${\int_{0}^{4}𝑓(𝑥)𝑑𝑥}$$は「曲線$${y=𝑓(𝑥)}$$，$${𝑥}$$軸，直線$${𝑥=0}$$，直線$${𝑥=4}$$」の4つで囲まれた図形の符号付き面積ですが、今回の記事ではシンプルに「面積」と捉えてしまった方がスッキリ分かると思います。

一般に、$${𝑥}$$を別の$${t}$$の式で置き直すとグラフの形が横方向に変化し、それに伴って面積が変化します。下の図を眺めてみましょう。

左下の面積(★)を実際の面積(☆)に「補正」するには全体を2倍、右下の面積(★★)を実際の面積(☆)に「補正」するには全体を$${\frac{1}{2}}$$倍すればよく、式で書くと次のようになります。

$${x=t^2}$$とおいた場合、図形が横方向に伸び縮みする割合が地点$${x}$$ごとに異なるので、最終結果をまとめて何倍かして「補正」することはできず、各地点$${x}$$に応じた「補正」をその都度おこなう必要があります。ただ、上の結果をふまえればその「補正」が

となることは、納得が行くと思います。この式、よく見ると(*)そのものです。

まとめると、「$${x}$$を使って『淡々と』面積を計算する代わりに、$${t}$$を使って『緩急付けて』面積を計算しよう」というのが、置換積分の「気分」です。感覚として理解できたでしょうか？

それでは、次の数学こぼれ話でお会いしましょう！

■大学入試情報を無料でお届けします！

■対話シリーズを含む「数学こぼれ話」
　過去の記事はこちら

■入試問題分析・解法に関する記事はこちら