
数学こぼれ話#24 実社会シリーズvol.5 ~データの不正を数学で暴く!~
今年もY-SAPIX数学科をよろしくお願いします。
さて、高校数学で現実世界を切り込む「実社会シリーズ」が第5弾を迎えました。今回は「指数・対数×会計学」と題して、「ベンフォードの法則」を見てみましょう。1938年に提唱された法則ですが、人間の直感を大きく裏切るような内容であり、初めて知ったときの衝撃は相当なものです。
■SAPIXメソッドを活かした大学受験塾!Y-SAPIXって知ってる?
【クイズ】
今、あなたの手元には、日本に関する統計データが大量にあるとします。その中身は「ある会社の5年分の株価」「日本全国の市町村別人口」「直近10年間のキャベツ生産量」など、それらを表す数値が手元に大量にある状態です。様々な長さの数値がありますが、その先頭の数字は1~9の9種類しかありません。さて、これらの数値からランダムに10000個を選んだとき、これらの先頭の数字はどういう分布をしているでしょうか? やはり、1~9が満遍なく出るでしょうか。あるいは、何か特定の数字が出やすいでしょうか。
〇近似して扱いやすく
精密な証明をするには数学Ⅲ以降の道具が必要になってしまうので、ここでは全ての数値を「$${\gdef\bar#1{#1^n} \bar{2}}$$($${n}$$は正の整数)」で近似することにしましょう。例えば、東京都の人口は1400万人程度ですが、これは$${2^{24}=16777216}$$で近似します。$${2^{50}}$$は約1000兆で、日本の国家予算は約100兆円ということを考えれば、$${\gdef\bar#1{#1^1} \bar{2},\gdef\bar#1{#1^2} \bar{2},…,2^{50}}$$で近似しておけば十分でしょう。いま皆さんの手元には、このような数値が大量にある状態です。(※「箱から取り出すタイプのくじ引き」を想像するとよいです。)
■高校数学をより深く使い、「一歩先の数学」の世界へ!
〇証明をしてみよう
では、さっそく証明をしてみましょう。少し難しいですが、頑張ってついてきてください!
ここから1つの数値をランダムに取り出し、それ$${\gdef\bar#1{#1^n} \bar{2}}$$をとします。もちろん、$${n}$$は1~50のいずれかです。さて、この数値が「先頭3」となるのは、$${n}$$が$${3×}$$$${\gdef\bar#1{#1^m} \bar{10}}$$$${≤\gdef\bar#1{#1^n} \bar{2}<4×\gdef\bar#1{#1^m} \bar{10}}$$、つまり$${\dfrac{log3+m}{log2}≤n<\dfrac{log4+m}{log2}}$$を満たすときです。ここでは、10を底とする常用対数を使っています。
この「幅」を計算すると$${\dfrac{log4-log3}{log2}}$$なので、$${m}$$の値には無関係と分かります。ややこしくなってきたので、下の図でイメージを掴みましょう。
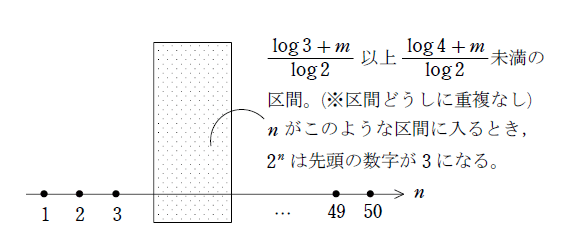
1~50が並んだ数直線上に、「先頭1のゾーン」「先頭2のゾーン」…「先頭9のゾーン」が順に並び、これが終わったら、また「先頭1のゾーン」…と繰り返されます。1セットが終わった後に繰り返しが起こることは、logの性質から$${log10+m=log1+(m+1)}$$が成り立つことを見れば分かりますね。
1セット分の「幅」を計算してみると
$${\dfrac{log2ーlog1}{log2}+\dfrac{log3-log2}{log2}+…+\dfrac{log10-log9}{log2}=\dfrac{1}{log2}(≒3.3)}$$
なので、ランダムに取り出した$${\gdef\bar#1{#1^n} \bar{2}}$$の先頭の数字が3になる確率、言い換えれば、ランダムに選んだ$${n}$$が「先頭3のゾーン」に含まれる確率は、およそ$${log4-log3}$$ということになります。一般的に考えれば、$${\gdef\bar#1{#1^n} \bar{2}}$$の先頭の数字が$${k}$$(※1~9のいずれか)となる確率は、$${log(k+1)-logk}$$となることが分かりますね!
■大学受験、選ぶなら。
〇先頭の数字は何になりやすい?
ようやく、冒頭の【クイズ】に答えられそうです。先ほどの結果をグラフにすると、次の通りです。見やすくするために、間を結んでひとつの曲線にしています。

ということで、【クイズ】の正解は
「1が一番出やすい。2,3,…,9となるにつれて、だんだんと出づらくなる。」
でした! 取り出した10000個の内訳は、先頭1の数値が約3000個、…、先頭9の数値が約400個といった具合です。
皆さん、正解できていましたか?(というのは冗談で、このことが「直感的」に分かるとしたら、途方もない智力の持ち主と言ってよいです。なぜなら、この法則が提唱されたばかりの頃は、多くの数学者や物理学者が大いに不思議がり、その証明に挑んだのですから。)
〇数学の力で不正を暴く!
先ほどの証明が分かれば、法則の仕組みは大体分かったようなものです。しかし、それでも「ベンフォードの法則」は不思議に感じられると思います。その理由は、やはり「直感に反すること」にあるのでしょう。この法則は、企業が公表しているデータに不正が無いかをチェックするのに使われており、実際に摘発された事例が何件もあります。「生のデータ」を改ざんするとき、人はどうしてもランダムな数字を使いたくなるものです。ところが、そうして作られたデータは「ベンフォードの法則」に従っていないので、不自然なのです。数学的な事実が思いがけず実社会で役立つということの、象徴的な例ですね。
それでは、次の「実社会シリーズ」で再びお会いしましょう!
■\的中/2024年京都大学(理系)数学,解法がそっくりだった件。
■大学入試情報を無料でお届けします!

■大学受験の総合情報サイト→ぜひホーム画面に追加してご確認ください!
■対話シリーズを含む「数学こぼれ話」過去の記事はこちら
■入試問題分析・解法に関する記事はこちら
■Y-SAPIXで数学を始めよう!

