皆さん、こんにちは。
Y-SAPIX数学科がお届けする数学こぼれ話、第33弾にあたる今回の記事では「置換積分」について、少し深く見ていきましょう。

〇tanによる置換積分

数学Ⅲを学習している方であればよく出会う定積分に、$${\int_{0}^{1 }{\frac{1}{{1+x^2}}} dx}$$というものがあります。まずは、典型的な計算方法を復習しておきましょう。

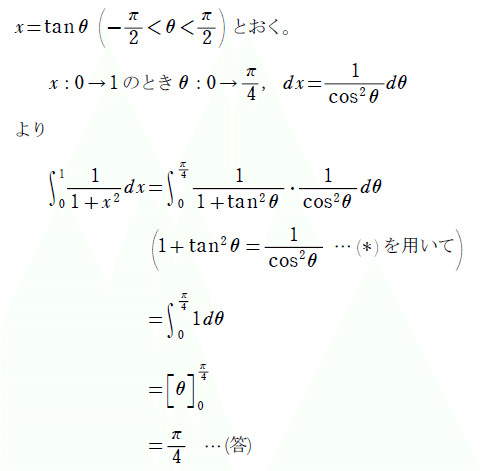
数学Ⅲの授業で初めてこの方法に出会うと、まるで狐につままれたようになる生徒もいます。特に質問が出なければ、「今まであまり活躍の場がなかった相互関係(*)が活躍してよかったですね！」程度のコメントで済ませますが、時には「なぜtanを使うと上手くいくんですか？」という質問が出ます。なぜ、tanを使うと上手くいくのでしょうか？

〇tanxの逆関数を微分すると？

上のカラクリを見るために、まずtan$${x}$$の逆関数を$${f(x)}$$と書き、この導関数$${f'(x)}$$を求めてみましょう。(※実はArctan$${x}$$と書きます。)　逆関数の微分法を思い出せば、問題ありません。

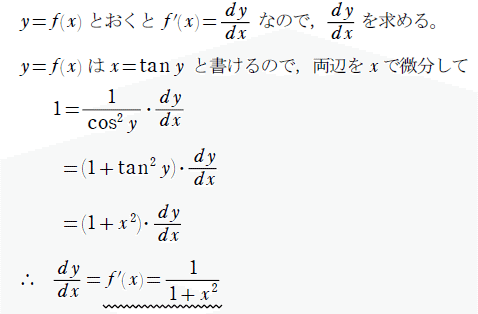
〇逆関数を使って計算してみよう！

波線部分をよく見ると、どうやら$${f(x)}$$さえあれば、$${\int_{0}^{1 }{\frac{1}{{1+x^2}}} dx}$$を計算できるようです。(※$${\frac{1}{1+x^2}}$$を積分するには、微分すると$${\frac{1}{1+x^2}}$$になる関数をひとつ見つければよい、ということを思い出しましょう。今回は、それが$${f(x)}$$というわけです。)　そのため、計算は次の通り「直接的」に行えることが分かります。

結局、最初に示した計算方法での$${x}$$=tan$${\theta}$$は、上の□囲みあたりを避けるために、先に「下処理」をしているに過ぎません。同じような事情は、$${\int_{0}^{\frac{1}{2} }{\frac{1}{\sqrt{1-x^2}}} dx}$$などの計算(※$${x}$$=sin$${\theta}$$のように置換する)にも見られます。こちらは、今度は「sin$${x}$$の逆関数」が絡んでいるのです。

(余談ですが、このような「逆三角関数の微積分」は、理工系の大学1年生で学習します。興味本位で調べた限りでは、いわゆる「高校数学」の範囲内でこれが教えられていた時代は無いようです。)
 
それでは、次の数学こぼれ話でお会いしましょう！

■大学入試情報を無料でお届けします！

■大学受験の総合情報サイト
→ぜひホーム画面に追加してご確認ください！

■対話シリーズを含む「数学こぼれ話」
　過去の記事はこちら

■入試問題分析・解法に関する記事はこちら