
数学こぼれ話#31 ~複素数を使って初等幾何を楽しもう!~
皆さん、こんにちは。Y-SAPIX数学科がお送りするシリーズ第31弾は「複素数×初等幾何」と題し、複素数平面の知識を活用して、正$${n}$$角形にまつわる美しい事実を導きたいと思います。高3理系数学の授業で先日出た話題ですが、「複素数の強力さ」を再確認することができました。(※この記事では、数学C「複素数平面」の知識を前提とします。)
【問題】
半径1の円に内接する正$${n}$$角形は、辺と対角線を合計で$${\frac{n^2-n}{2}}$$本持ちます。これらの長さを全部かけた値は、どのような「$${n}$$の式」で表されるでしょうか?
〇n次方程式を解く
まず、$${n}$$次方程式$${z^n=1}$$を解いてみましょう。両辺の絶対値をとると$${|z|=1}$$が分かるので、解は$${z=\cos \theta+i\sin \theta(0≦\theta<2\pi)}$$のように書けます。これを元の方程式へ代入すると、次のような計算を経て、$${n}$$個の解全体が得られます。

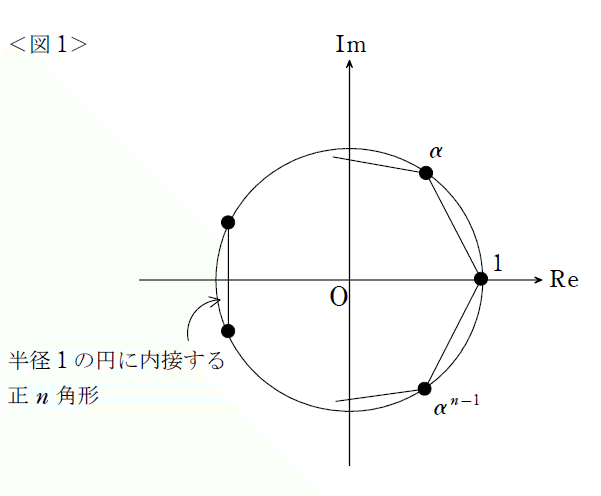
これら$${n}$$個の解は、全て大きさが1なので、複素数平面内の単位円上にあることが分かります。さらに、偏角は0から$${\frac{2\pi}{n}}$$ずつ増えていくので、円周を反時計回りに$${n}$$等分していることも分かります。表記を簡単にするために$${\cos \frac{2\pi}{n}+i\sin \frac{2\pi}{n}=α}$$と置けば、これらの解は$${z=1,α,α^2,…,α^{n-1}}$$のように書けて、複素数平面上では<図1>のようになります。
〇役に立つ恒等式を作ろう
複素数平面内に正$${n}$$角形が作られ、なんとなく【問題】の解決に近づいてきた感じがします。次に$${1,α,α^2,…,α^{n-1}}$$は$${z^n=1}$$つまり$${z^n-1=0}$$の相異なる解なので、左辺の因数分解に注目して、次のようにして恒等式(*)を得られます。
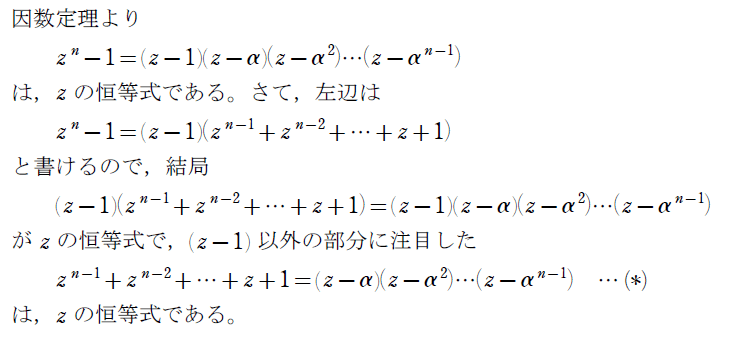
<図1>と(*)を見比べると、<図2>のような話を進めることができます。


(#)の左辺に現れる$${n-1}$$個の絶対値は、図の太線に示したような$${n-1}$$本の辺および対角線の長さを表しています。つまり(#)は、「正$${n}$$角形の1頂点から延びる$${n-1}$$本の辺および対角線の長さを全てかけた値は$${n}$$である」と読み取ることができます。
あとは、他の頂点でも同じようにすれば、【問題】の解決はもう間近です。安直に考えると「$${n^n}$$?」に思えますが、この計算では<図2>に書いたような長さ$${L}$$を2回かけていることに注意しなければなりません。(他の線分でも、事情は全く同じです) 実際には、1本の長さを1回ずつかけるだけなので、【問題】に対する答えは$${\sqrt{n^n}}$$ということになります。
〇複素数と初等幾何
「半径1の円に内接する正$${n}$$角形の辺および対角線の長さを全部かけると$${\sqrt{n^n}}$$になる」という、初等幾何の美しい事実が得られました! これに限らず、初等幾何の問題を複素数平面で上手く扱うと、初等幾何にありがちな「発想のハードル」を大幅に下げられることが多くあります。(もちろん、そのぶん「複素数平面」に習熟している必要がありますが、こちらは訓練でどうとでもなるので些細な問題です)「初等幾何×複素数」というテーマでは他にも面白い話題がたくさんあるので、興味のある方は是非いろいろと調べてみてください。
それでは、次のこぼれ話でお会いしましょう!
■大学入試情報を無料でお届けします!

■大学受験の総合情報サイト
→ぜひホーム画面に追加してご確認ください!
■対話シリーズを含む「数学こぼれ話」
過去の記事はこちら
■入試問題分析・解法に関する記事はこちら

