皆さん、こんにちは。Y-SAPIX数学科では、「一歩先の理解」を目指す方々を対象に、「深掘りシリーズ」の記事を発信していきます。

今回のテーマは「数学的帰納法」です。様々な証明の場面で活躍するこの論法について、仕組みの確認から発展的な話題まで、幅広く見ていきましょう！

〇帰納法の仕組み　～あらゆるnを切り返すには～

数学的帰納法は、よく「ドミノ倒し」に例えて説明されます。それでもよいのですが、ここでは少し違った角度から眺めてみましょう。数学を学ぶうえで大切な「任意に固定」という感覚も分かると思います。

さて、突然ですが今あなたは人々の前に立って、正しいと信じてやまない
  「全ての自然数$${n}$$で、$${2^n \geqq n+1}$$が成り立つ」
という事柄を主張したとします。(だいぶ変な状況ですが、ご容赦を)
目の前の人々はかなり疑り深く、「$${n=5}$$で成り立つのか？」「$${n=10}$$で成り立つのか？」と次々に尋ねてきます。挙句の果てには「$${n=100}$$で成り立つのか？」などと言い始めますが、まさか手計算で$${2^{100}}$$を求めるわけにもいきません。しかし、ありとあらゆる$${n}$$を対処できなければ、主張は取り下げなければならないでしょう。さて、どうしましょうか？

1つの切り返し方として、次のような事柄が言えれば「勝ち」です。
　　1°　 $${n=1}$$で成り立つ　【$${p(1)}$$】
　　2°　（$${k}$$は何らかの自然数として)
　　　もし$${n=k}$$で成り立つならば、必ず$${n=k+1}$$で成り立つ【$${p(k) \implies p(k+1)}$$】
　※答案としての書き方は、教科書や問題集で確認しましょう。

　ともあれ、上の事柄さえ言えてしまえば、「$${n=100}$$で成り立つのか？」という質問には、こう切り返せるのです。

「では、今からチェック用の装置を渡すので、これを使ってください。まず、$${n=1}$$で成り立つので、2°を使えば$${n=2}$$で成り立ち、計算は不要です。2°を使えば、$${n=3}$$で成り立ち、計算は不要です。後は、同じことを繰り返せば、$${2^{100}}$$と$${100+1}$$を実際に計算するまでもなく$${n=100}$$で成り立っています。」

上の切り返しは$${n=100}$$だから出来たことではなく、どんな自然数$${n}$$にも通用することが分かりますね。これにて、あらゆる批判に耐えうる主張として、その正しさは人々に認められることとなりました。

〇二重帰納法　～平面内で広がってみよう～

さて、ここまで見てきた皆さんなら「数学的帰納法」というものを
　　「あらゆる$${n}$$に対して、自動チェックを進められる装置」
として、心から理解できているはずです。

ところでこの装置は、「$${p(1) \implies p(2) \implies p(3)\implies\ldots}$$」というように、直線的なチェックを進めるように見えます。では、次元を1つ上げた「平面的」な帰納法──「二重帰納法」──は、どのように組み立てるとよいのでしょうか？ 次の＜問題＞を考えてみましょう。

＜問題＞
任意の自然数$${m,n}$$に対して、ある命題$${p(m,n)}$$が真であることを証明するには、どのように数学的帰納法を組み立てるとよいか。
※　ヒント　$${xy}$$平面の第一象限内に広がる格子点$${(m,n)}$$を想像する

＜考え方＞

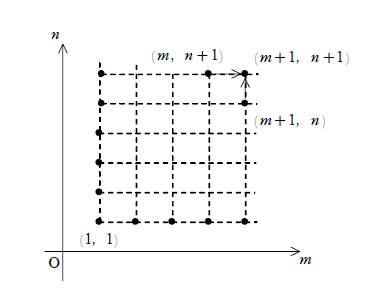
1°　$${p(m,1),p(1,n)}$$　($${(m,n)}$$は任意の自然数)
2°　$${ \begin{cases} p(m+1,n) \\ p(m,n+1) \end{cases} \implies p(m+1,n+1)}$$
が言えれば、1°と2°を繰り返し使うことで、任意の$${(m,n)}$$に対して、$${p(m,n)}$$が確認される。（※2°の部分は、他の形でもOK）

結局、数学的帰納法の本質は「自動でチェックを進める装置」ということが分かりました。数学的帰納法は背理法と並ぶ非常に強力な証明法ですので、様々な論証問題を通じてマスターしておきたいものです。

それでは、次回の「深掘りシリーズ」でお会いしましょう！