皆さん、こんにちは。

Y-SAPIXでは新高校3年生(現高校2年生)対象の「東大・最難関大数学」という講座を、2022年1月から対面／オンラインで開講しています。東大・京大・東工大を始めとする最難関大の出題を攻略できる実力が身につくためには、どのような姿勢で数学を学習していくとよいのでしょうか？ 2021年秋に実施した特別講座「高2東大特訓」の内容と結びつけながら、そのヒントをお伝えしていければと思います。

3日目のテーマは「場合の数・確率」です。

今年の東大入試では、理科数学では6年ぶりに、文科数学では3年ぶりに確率分野から出題されました。「なんとなく解けるけれど、立てた式にいまひとつ自信を持てない…。」「解答を読めば分かるけれど、自分の方法でなぜ答えが合わないのかしっくりこない…。」という声が聞こえてきやすい分野です。そこで、今回の記事では「確率」に的を絞り、考え方を再確認していきましょう。

〇自分の理解と向き合うこと～基礎編～

今回は少し趣向を変えて、「確率をあまり知らない人に、自分なりに説明しよう」という切り口で進めていきます。授業をはじめ、誰かに何かを説明する場面では「こういうものだから」が通用せず、その事柄を自分の中で噛み砕いて理解できているかが問われます。そのため、説明するという行為を通じて自分自身の理解がいっそう深まるのを実感し、「自分のためにもなったな」という気持ちになります。

ここでは、皆さんにもそのような体験をしてもらい、確率に対する理解を深めることを目指します。まずは＜問い＞だけを読み、自分ならどう説明するかを考えてみましょう。考えがまとまったら、画面をスクロールして＜回答例＞を確認してみましょう。では、始めます。

＜問い＞
①場合の数で出てくる「～通り」と、確率で出てくる「～通り」の違いは何　か。
②次のような道路で、地点Ａから地点Ｂまで最短経路で進む点Ｐを考える。ただし、点Ｐは交差点にのみ存在し、複数の道路を選べるとき、それぞれの道路を等しい確率で選ぶとする。

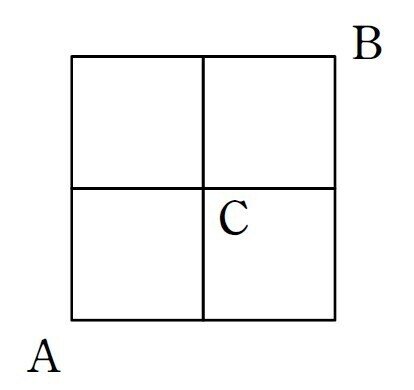
点Ｐが地点Ｃを通る確率を次のように求めるのは、どのように誤っているか。また、正しい確率を求めよ。
　「ＡからＢまでの最短経路は６通り。うち、Ｃを通る最短経路は２×２=４通り。よって、求める確率は$${\frac{2}{3}}$$」

＜回答例＞
①例えば、６つの面が「１，１，１，２，２，３」で、どの面も等しく出やすいサイコロを考える。
いま、サイコロを1回振ったときに出る目の全パターンを考える。場合の数で問われるのは「異なる景色の数」なので、「１が出る」「２が出る」「３が出る」より、３通り。一方、確率を求めるときには「起こりやすさ」(景色としての珍しさ)まで考慮しなければならない。１は３よりも３倍出やすく、したがって、全パターンは例えば  １×３+１×２+１×１=６通りなどとする。ただし、「３が出る」を基準(つまり、「１通り」扱い)としたが、基準は本来どこに置いてもよい。
②全ての経路は「→→↑↑」のように、２個の→と２個の↑の並びで表される。このうち、大きな正方形の４辺上に点Ｐがあるとき、経路の選び方が自動的に決まってしまう。そのため、例えば「↑↑→→」と「→→↑↑」は、他の４経路(例えば、「↑→↑→」)よりも２倍起こりやすい。よって、起こりやすさを考慮したとき、ＡからＢまでの最短経路は １×４+２×２=８通りである。
うち、Ｃを通る最短経路は １×４=４通り
なので、点Ｐが地点Ｃを通る確率は$${\frac{1}{2}}$$である。

いかがでしょうか？ 「当たり前」で済ませてきたことを真正面から問われて、驚いたかもしれませんね。
(実は、ハッとしてもらうことが狙いなのでした。) この調子で、どんどん進めていきます。

〇自分の理解と向き合うこと～応用編～

では、もう少し実戦的な話題に移っていきます。移り変わる状態を扱うために「確率漸化式」を使うときの鉄則は
１°状態の移り変わりを眺め、「一定のパターン」が現れている様子を見抜く。あるいは、一定のパターンが現れるよう、複数の状態を「ひとつの状態」として扱う。
２°ある状態から別の状態に移る「推移の確率」を捉える。
３°「(全確率)=１」を含む確率漸化式を立て、数列の議論に持ち込んで漸化式を解く。
でした。ここでは、３°と関わる部分について確認しましょう。

＜問い＞
次のような正四面体ＡＢＣＤの頂点を１秒ごとに移動する点Ｐについて考える。ただし、点Ｐは最初Ａにあり、隣り合う頂点に等しい確率$${\frac{1}{3}}$$で移るとする。 $${n}$$ 秒後に点ＰがＡにある確率を$${a_n}$$とする。B，C，Dについても同様に$${b_n}$$，$${c_n}$$，$${d_n}$$と定める。

このとき、等式「$${a_{n+1}}$$=$${\frac{1}{3}{b_n}}$$+$${\frac{1}{3}{c_n}}$$+$${\frac{1}{3}{d_n}}$$」が成り立つのは何故か。
＜回答例＞
「$${n}$$+1秒後に点ＰがＡにある」という出来事を考える。定義より、この確率は $${a_{n+1}}$$　…①
一方、この出来事は
「$${n}$$秒後に点ＰがＢにあり、確率$${\frac{1}{3}}$$でＡに移動する」
「$${n}$$秒後に点ＰがＣにあり、確率$${\frac{1}{3}}$$でＡに移動する」
「$${n}$$秒後に点ＰがＤにあり、確率$${\frac{1}{3}}$$でＡに移動する」
 という３つの出来事へ細分化でき、その確率は

$${\frac{1}{3}{b_n}}$$+$${\frac{1}{3}{c_n}}$$+$${\frac{1}{3}{d_n}}$$　…②

①と②は同じ出来事の確率を表すので、値として等しく

$${a_{n+1}}$$=$${\frac{1}{3}{b_n}}$$+$${\frac{1}{3}{c_n}}$$+$${\frac{1}{3}{d_n}}$$　…③

である。

結局、「$${n}$$+1秒後の出来事」を、「$${n}$$秒後の状況」という観点から捉え直すことで、①と同じ確率の数値に、②という別の表し方を与えたことになっている。したがって、例えば「1秒後の状況」という観点から捉え直し、③のような確率漸化式を立てるケースもあり得る。そのような場面で右辺に現れる$${a_n}$$，$${b_n}$$，$${c_n}$$ などは「$${n}$$秒後」という記号本来の意味からは離れ、「値として同じなので利用している」以上の意味を持たないことに注意したい。

〇自分の解答と向き合うこと

さて、「応用編」としては「対称性や対等性」「モデル化と一対一対応」など語りたいことはまだまだあるのですが、今回は一旦これくらいにしておきます。#２の整数もそうですが、場合の数・確率に代表されるような「離散分野」は、要求される知識こそ少ないものの、上手に学習を進めづらいのも事実です。「決まりきったやり方」が無いぶん、自分なりの方法で取り組むことができ、それゆえ冒頭にお伝えしたような「釈然としない気分」が生じやすいのです。

このような分野を学習するとき、皆さんには是非

答えが合わなかったときに、自分の解法に潜む原因を追究すること

を心がけてほしいと思います。間違えた解答と根気よく向き合うことで初めて根本的な事柄への理解が深まり、自然と答えが合うようになっていく、そういう分野です。一歩一歩、着実に進んでいきましょう。

#１から続いてきた 「こぼれ話」は、ここで一区切りとなります。ここまでお付き合いいただいた皆さん、ありがとうございます。

4月以降も定期的にY-SAPIX数学科からnote記事を発信していく予定ですので、どうぞお楽しみに！