
数学こぼれ話#2/背理法を深掘り
皆さん、こんにちは。
Y-SAPIXでは新高校3年生(現高校2年生)対象の「東大・最難関大数学」という講座を、2022年1月から対面/オンラインで開講しています。
東大・京大・東工大を始めとする最難関大の出題を攻略できる実力が身につくためには、どのような姿勢で数学を学習していくとよいのでしょうか?
2021年秋に実施した特別講座「高2東大特訓」の内容と結びつけながら、そのヒントをお伝えしていければと思います。
2日目のテーマは「整数」です。
整数といえば「論証」ということで、授業の冒頭では
「対偶証明法」「背理法」「数学的帰納法」
といった、代表的な間接証明の仕方について確認しました。その後は、2019年度東京大学入試問題 数学(理科)第4問のアレンジを含む全問オリジナルのテキストを使った演習です。
背理法について
論証の場面で活躍する背理法について、確認しておきましょう。
背理法とは、
「ある命題は真である」ことを主張するために ① 結論を否定する ② 何らかの矛盾が導かれる ③ よって、否定する前の結論が正しい の三段階で運ぶ論法である。
以上のことは、多くの方がご存知でしょう。では、問題です。
__________________________________【問題】
「『$${p}$$ならば$${q}$$』は真である」ことを背理法で主張するときの、証明の書き出しにあたるものは何か。$${p}$$や$${q}$$を用いて答えよ。
__________________________________
いかがでしょうか?
背理法で証明するときの出発点は「結論の否定」でした。
「命題『$${p}$$ならば$${q}$$』では$${p}$$を仮定、$${q}$$を結論と呼ぶので、書き出しにあたるものは$${q}$$の否定、つまり$${\bar{q}}$$です。」と答えてくれる方が沢山いますが、これは誤りです(ちなみに、大学以降の論理学では、$${q}$$の否定を「$${\bar{q}}$$」ではなく「$${\neg{q}}$$」と書くのが一般的です)。
しかし、冷静になってみると、代わりに「『$${\bar{q}}$$ならば$${\bar{p}}$$』は真である」ことを主張する対偶証明法での証明の書き出しにあたるものは、$${\bar{q}}$$ですね。
ということは、背理法と対偶証明法は、全く同じものということになってしまいます。ここでのポイントは、否定の対象である「結論」とは何なのか? ということです。
自分なりに納得し、使うこと
答えを先に言ってしまうと、「『$${p}$$ならば$${q}$$』は真である」ことを背理法で主張するときの、証明の書き出しにあたるものは$${\bar{q}}$$ではなく、$${p}$$かつ$${\bar{q}}$$です。これだけでピンと来ることはまず無いと思いますが、集合を使うと直感的に理解することができます。
さて、$${p}$$を満たす要素の集合(真理集合)を$${P}$$のように定めると
「$${p}$$ならば$${q}$$」は真である $${\Longleftrightarrow}$$ $${P}$$は$${Q}$$に含まれる ($${P \subset{Q}}$$)
という対応関係が成り立ちます。
「東京在住ならば関東在住」は真である
$${\Longleftrightarrow}$$ 東京は関東に含まれる(東京$${\subset}$$関東)
のように考えれば納得できるはずです。集合を使って「行間」を埋めてみるとしましょう。
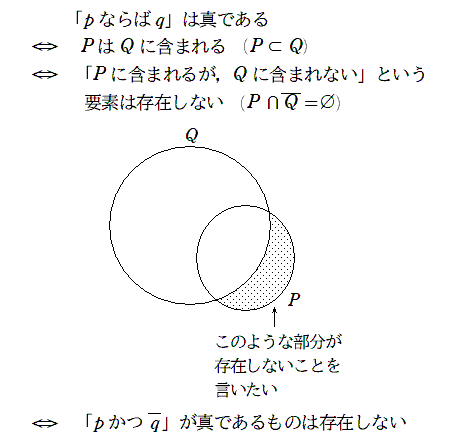
背理法で主張するときの証明の書き出しにあたるものが「$${\bar{q}}$$」ではなく「$${p}$$かつ$${\bar{q}}$$」ということが納得できたでしょうか?
強力な論法として幾度となく使ってきた背理法も、改めて考えると奥が深いのです。
もちろん、背理法そのものへの理解が曖昧でも問題は解けますし、仕組みを完璧に理解しなければ背理法を使ってはならない、ということでもありません(真理集合$${P}$$が考えられない条件$${p}$$も世の中にはあるので、集合を使った直感的な「説明」は、残念ながら「証明」とするには不十分です。数学的な厳密さを追究するならば、「真理値表(Truth table)」を使ったり、論理式の変形を運んでいった方がずっと正確です)。
しかし、ここでお伝えしたいのは...
自分なりに書いた証明に、もし、
「本当にこれで大丈夫だろうか?」という気持ちを抱いたときは、
その気持ちを大切にしてほしい
ということなのです。
こういった問いかけは手ごわいことがほとんどですが、授業内でのやりとりや自主的な調べ学習を通じて自分なりに納得すれば、前よりも深く理解しながら「道具」を使うことができます。
こういう経験を積み重ねていければ、見慣れない問題を自力で解決するために必要な「本当の実力」が身についていくはずです。
また、必要条件・十分条件をはじめとする様々な概念は、「命題と論証」の単元で習って終わりではなく、心から納得して数学を学習していくために欠かせない土台の部分です。
「東大・最難関大数学」をはじめとする高校3年生の授業では実戦的な問題を多く扱いますが、だからこそ、1題1題をバラバラに理解するのではなく、「多くの問題を見通し良く解決するために必要な眼力を養うこと」を大切にしています。
さて、次回はいよいよ「高2東大特訓編」の最終回を迎えます。
3日目のテーマ「場合の数・確率」でお会いしましょう!

