今回のテーマは「積分法」です。面積を計算できる図形の幅が格段に広がる素晴らしい単元ですが、「なんとなくモヤッとする…」となりやすい単元でもあります。数Ⅱの大トリである積分法、この機会に疑問点を解消してしまいましょう。少し進んだ内容も含まれるので、得意な方も必見です！

定積分≠面積

さて、さっそく確認すると

定積分と面積は別物

なのは、大丈夫でしょうか？ 確かに、定積分を計算して負の値が出てくることはよくありますね。しかし、放物線と直線で囲まれた図形の面積を求めるときに使うのも定積分です。

高校数学での積分といえば「微分の逆操作」、つまり微分して$${f(x)}$$に「戻る」ような関数$${F(x)}$$を探してきて…という流れが定番です。この流れはシンプルで分かりやすいものの、なんとなく無味乾燥な印象を抱きがちです。形式的な操作を繰り返すうちに計算は出来るようになりますが、いつの間にか「そういえば、なぜ定積分で面積が求まるんだっけ？」となってしまうのも、頷けます。

２つの流派　～定積分の「定義」をめぐって～

$${\ \displaystyle \int_a^b f(x)dx }$$

という記号には「高校流の定義」と「大学流の定義」の2つがあります。

一言でまとめるなら

「初めに原始関数あり」なのが、高校流
「初めに符号付き面積あり」なのが、大学流

という風になります。

$${\ \displaystyle \int_a^b f(x)dx }$$=$${F(b)}$$$${-}$$$${F(a)}$$

で計算されるのが定積分だ、というのが高校流の定義です。こちらは学校で習う通りですので、慣れている人も多いと思います。

一方で、「符号付き面積」というキーワードは、初めて聞いた方が多いかもしれませんね。
次の見出しで、簡単に流れを掴んでみましょう。

「符号付き面積」として捉えてみよう

まず、「符号付き面積」の説明から。頭の中に$${xy}$$平面を浮かべ、閉じた図形をひとつ置いてください。このとき、$${x}$$軸より上側にある部分は「符号付き面積：プラス」、$${x}$$軸より下側にある部分は「符号付き面積：マイナス」と定義します。下の図も参考にしてください。

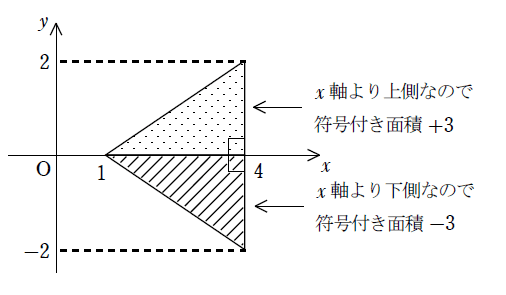
次に、「曲線$${y=f(x)}$$，$${x}$$軸，直線$${x=a}$$，直線$${x=b}$$」の4つで囲まれた領域を考えます。
1つ1つの議論は大変なので省略しますが、結果として

打点部の「符号付き面積」は確定している

ことが分かり、その値を

$${\ \displaystyle \int_a^b f(x)dx }$$

と書くことにします。前の見出しで書いた「初めに符号付き面積あり」というのは、こういう意味です。さらに、$${F'(x)=f(x)}$$を満たす関数$${F(x)}$$を使えば、その値は

$${\ \displaystyle \int_a^b f(x)dx }$$=$${F(b)}$$$${-}$$$${F(a)}$$

という計算で求まる、ということを導けます。こちらも、下の図を参考にしてください。

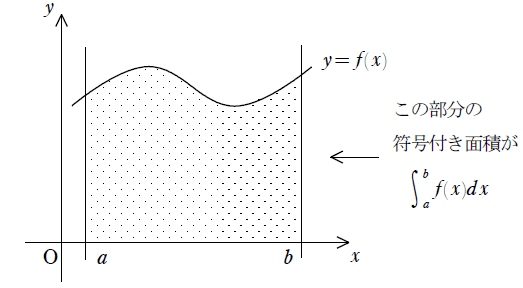
ひとつの例　～絶対値付き定積分～

先ほどの内容を一言でまとめると、

$${\ \displaystyle \int_a^b f(x)dx }$$

が表すのは

曲線$${y=f(x)}$$，$${x}$$軸，直線$${x=a}$$，$${x=b}$$で囲まれた部分の符号付き面積

である、と言うことができます。「符号付き面積」というところを改めて強調しておきます。
このような見方が身に付いてくると、例えば

$${\ \displaystyle \int_0^3 \lvert x-1 \lvert dx }$$

という定積分を求めるには、以下のような図を描くのが自然な方法だ、と思えるでしょう。
なぜなら、問われているのは上の定義通り

曲線$${y=|x-1|}$$，$${x}$$軸，直線$${x=0}$$，$${x=3}$$で囲まれた部分の符号付き面積

なのですから。

これを「高校流」にこだわってしまうと、まず$${F'(x)=|x-1|}$$となる関数$${F(x)}$$を探すところから始めなくてはなりません。実際、例えば

$${F(x)=}$$$${\begin{cases}{-\frac{1}{2}x^2+x (x≦1)}\\{\frac{1}{2}x^2-x+1 (1≦x)}\end{cases}}$$

を使うと

$${\ \displaystyle \int_0^3 \lvert x-1 \lvert dx }$$=$${F(3)}$$$${-}$$$${F(0)}$$=$${\cdots}$$

と計算できますが、肝心の$${F(x)}$$を求めるところが非常に大変です。

さて、今年度の数学こぼれ話はここまでとなります。1年間お付き合いいただき、ありがとうございました。4月以降の記事で、再びお会いしましょう！

■Y-SAPIXで数学を始めよう！