2021年度個別試験における、主要大学の出題傾向と回答のポイント、対策を科目ごとにご紹介します。

第3回は数学。

2022年度の入試対策としてお役立てください。

１．全体的な傾向

近年の大学入試数学の流れを一言で言うと「易化傾向」といってもよいと思
います。誰もが試験時間内に解くことができないような問題は、ほとんど見られなくなり、かつてはかなりハイレベルな出題をしていた大学の問題でも、標準的な問題が中心になってきています。これは2017年の東京大学（理科）の入試が、近年まれに見る易しい問題だったことと無関係ではないでしょう。問題の難易度を上げると全受験生の得点が低くなり、入試結果に数学が影響しないことになります。その一方で、大学入試問題とは、その大学を目指す人にとって受験勉強を行うときの大きな目標という役割もあります。それがあまり易しいと、すぐに解けるようになり、がんばって勉強しようという気もおきなくなるものです。このあたりのバランスが難しいところです。

さて、初めに主要大学の一昨年から昨年、昨年から今年の難易度の変化を見てみましょう。

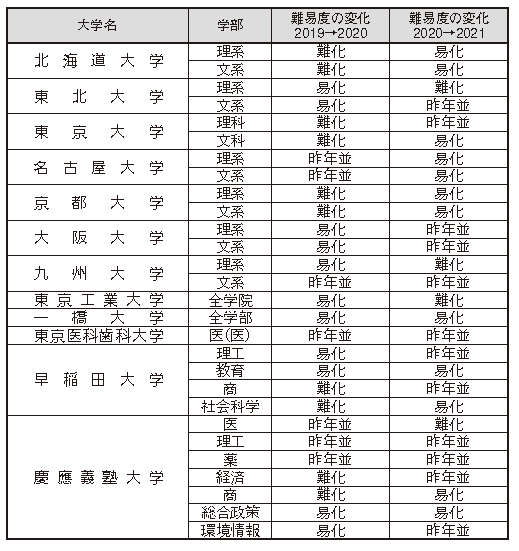
昨年の最大のトピックは、近年の易化傾向という大きな流れの中で、東京大
学と京都大学が共に難化したということでした。東京大学（理科）は、昨年難化したレベルを保ったまま高度な出題でしたが、その一方東京大学（文科）は典型的な問題もあり、今年は易化しました。京都大学は、理系文系共に標準的な問題が中心で易化しました。

昨年のもう一つの大きなトピックとしては、多くの大学が易化傾向にある中高度な出題を続けてきた、東北大学（理系）、東京工業大学、大阪大学（理系）、九州大学（理系）などの大学がそろって易化したことでした。ついにここまで来たかという感じがしたものです。しかし今年、東北大学（理系）、東京工業大学、九州大学（理系）は難化しました。大阪大学（理系）も、難化とまではいわないものの、大阪大学らしい出題がいくつもありました。

文系の中では、早稲田大学（商）と慶應義塾大学（経）において高度な出題が続いており、注目に値します。

全体としては、易化傾向という大きな流れがまだまだ続いています。昨年までかなりハイレベルな出題が続いていた名古屋大学（理系）は、今年ついに易化しました。数学Ⅲの微積分の出題がないことも、その一因かもしれません。また、かつては文系ながらも高度な出題を続けてきた一橋大学では、易化した昨年よりもさらに易化しました。東京医科歯科大学（医）、早稲田大学（理工）、慶應義塾大学（医、理工）なども、易化した水準が今年も維持されています。昨年高度な出題だった慶應義塾大学（商）も、今年は取り組みやすくなりました。とはいえ、簡単になったわけではなく、これら主要大学がある一定以上の数学の力を求めていることに変わりありません。

そして、今年はなんといっても、数学Ⅲの出題の減少が目につきました。早稲田大学（理工）や東京工業大学のように、例年数学Ⅲからの出題がかなりの割合を占める大学でも1題2題ほどの出題になっています。この2大学だけではなく、全体的に数学Ⅲ、特に微積分からの出題は減少しています。
他にも注目の問題は次です。

東京大学（文理共通）4⃣、東京工業大学3⃣、九州大学（理系）3⃣が共通して、二項係数に関する整数の出題があり、どの問題も興味深い内容になっています。

複素数平面の出題が減少している印象ですが、東北大学（理系）5⃣は本格的な複素数平面の問題です。九州大学（理系）4⃣も複素数平面の問題で、相変わらず同学はこの分野において新しいタイプの問題を出題し続けてくれています。ちなみに、九州大学（理系）2⃣も複素数平面の問題です。

東京大学（理科）1⃣・（文科）3⃣は放物線の通過領域を図示する問題で、テーマは違いますが、一橋大学3⃣でも同様の議論が必要になります。東北大学（理系）4⃣は線分の通過領域の面積を求める問題です。

京都大学（文系）3⃣は、よくある問題に見えますが、少し設定を変えるだけで違う問題になるという確率の面白さを教えてくれます。

２．主要大学の動向

（1）東京大学（理科）
2003年から2017年まで出題されていた「場合の数・確率」は、今年を含め4年連続で出題されませんでした。来年出題されるかどうか注目したいところです。

また、同学では頻出である空間図形の問題もありませんでした。その代わりといってはなんですが、1、2で座標平面上に図形を図示する問題がありました。こちらは近年頻出の分野です。その意味では傾向は踏襲されていました。

全体的な難易度は、難化した昨年の水準が保たれています。とはいえ、2017年に最も易しくなり、徐々に難化してきた水準が保たれているだけで、過去のように誰もが試験時間内に解くことができないような難問は見当たりません。

1⃣は、放物線Cともう一つの放物線の交点に関する条件から、放物線Cの
通りうる範囲を求める問題です。条件から、三角形と直線が共有点を持つ条件に帰着されますが、共有点を持たない場合を求め、それ以外の部分を答えると良いでしょう。

2⃣は、一見すると複素数の問題ですが、それは（1）の計算のみです。（2）では、変数α、β、γが全て1以上2以下の実数ですから、同学の問題らしく変数が多いものの、一つずつ動かしていけば難しくはありません。そしてそれを図示して終わりです。近年、このように平面図形を図示する問題が同学の出題で目につきます。

3⃣は、定積分の計算問題ですが、なかなか大変な計算です。ただし、一つず
つは基本的なものばかりですし、他の問題と比べると解きやすいといわざるを得ませんので、試験ではこの問題は落とせません。

4⃣は、二項係数に関する整数の問題でした。異なる2021個のものから37個選ぶ組合せの総数を4で割り、その余りを求める問題です。珍しく小問が四つもあり、誘導に乗っていけばよく、あまり発想力を必要とはしません。（2）がポイントで、まず整数は小さい方から順に考えると、4で割った余りは、1、2、3、0、1、2、3、0、…と周期4で繰り返すことを注意しておきます。異なる4a＋1個のものから4b＋1個選ぶ組合せの総数を式で書いたときに、分母は4b＋1から一つずつ小さくした整数を1まで掛け合わせたもの（4b＋1の階乗）であり、分子は4a＋1から一つずつ小さくした整数を4（a－b）＋1まで掛け合わせたものとなります。分母分子とも4b＋1個の整数の積であり、大きい方から見ると、4で割った余りがともに1から始まっています。4で割った余りが2の数全てを考えると、分母分子で同じ数あり、2で約分すると分母分子が全て奇数になります。4で割り切れる数も全て考えると、分母分子で同じ数ありますが、これらは全て奇数とは限りません。そこで、4で約分した後全部まとめてよくよく見ると、異なるa個からb個選ぶ組合せの総数が出てくるという仕組みになっています。また、（2）や（3）が不正解にもかかわらず、（2）と（3）の結果を用いて（4）のみ正解した受験生は得点を得ることができたのか気になります。

5⃣は、平面上に一つ定点を与え、もう一つ動点を考え、この2点間の距離の2乗を値とする関数の問題です。この関数がある範囲で、最大値を取ることを示します。方針も一本道で、計算量も多くはないので、3に引き続きこのセットでは落とせない問題といえます。

6⃣は、文字定数を含む4次式が、有理数係数の2次式に因数分解できるように文字定数を定める問題です。（2）が決定的なヒントですが、その意図するところをつかむことが難しかったと思われます。多項式の展開や因数分解の計算なのですが、なんでも展開する癖のある人は大変な計算になります。できる限りかたまりは崩さずに、うまく計算できるかが大きなポイントでしょう。

（2）東京大学（文科）
3⃣、4⃣はそれぞれ理科の1⃣、4⃣との共通問題でした。近年は文理で共通の題材が扱われる場合、文科の問題が易化する傾向にありましたが、今年度は全く同じ問題が出され、文科の受験生にとっては厳しいものになったといえます。

1⃣は、3次関数のグラフで表される曲線と原点を中心とする半径1の円が、共有点を6個持つ場合の問題です。典型的な問題といえ、方針に迷うところはなく絶対に落とせない問題です。

2⃣は、1以上2N以下の整数から、ある条件を満たす相異なるN個の整数を選ぶ問題です。（1）では、連続する2個の整数を含まない場合を求めます。連続してはいけないのでN個それぞれの間がN－1個あり、そこに最低でも1個の整数がなくてはいけないと考えると、残りの整数があと一つになりますので、その一つを決めれば良いわけです。（2）では、連続するN－2個の整数の組を少なくとも一つ含む場合を求めます。いろいろな方法があると思いますが、左から見て連続するN－2個の組の最小の数がどこにあるかで場合分けすると、すっきりと解けます。

前述したように、理科では場合の数・確率からの出題が4年間ありませんが、文科では、今年も含めて3年連続で出題されています。特に、昨年と今年は、確率ではなく、場合の数の出題です。その意図するところを尋ねてみたいです。

全体として、文科独自の1や2は取りやすくなっています。理科との共通の2題は、文系としては厳しい問題ですが、どちらも小問に分かれていますので、前半を確保すれば、ある程度の得点は見込めます。結果として昨年よりも易化したといえます。

（3）京都大学（理系）
まず目を引くのが、1⃣だけでなく6⃣までもが、一つの大問の中で、問1・問2と二つの問題に分かれているところです。2019年のように、1⃣が問1・問2に分かれていることは、同学において今まで何度もありましたが、一つのセットの中で2題がそうなっていることは、大変珍しいことだと思います。一つの大問が（1）・（2）のように、ヒント・誘導のために分かれていることはありますが、ここでいう「問1・問2」は、問1と問2がまったく別の問題の場合のことです。6では一瞬、問1の結果を用いて、問2を解くのかと錯覚した受験生もいたのではないでしょうか。そもそも同学では、理系文系に関わらず、（1）・（2）といった小問の誘導を極力避ける方針が取られています。ヒントや誘導をつけると、全員が同じ発想で解くことになることを嫌い、自由な発想で問題に取り組めるためだと思われます。今年は、5⃣のみが（1）・（2）と分かれていますが、2⃣、3⃣、4⃣に小問はありません。

1⃣の問1は、空間内の平面に関する対称な点を求める問題です。ベクトルのみでも解答可能ですが、平面の方程式を用いた方がはやいでしょう。問2は、4種類の玉が入った袋から、一つ取り出して戻すという操作を行います。n回目の試行で初めて赤玉が取り出され、4種類全てが1回以上取り出される確率を求めます。n－1回目までの試行で、残りの3種類が全て1回以上取り出される確率を求めて、n回目に赤玉が出る確率をかけます。

2⃣は、曲線の接線の接点とx軸の切片の間の距離の取り得る値の最小値を求める問題です。方針に迷うところはなく、計算量も大したことはありません。このセットでは、必ず正解したい問題です。

3⃣は、無限級数の和を求める問題です。ここに出てくる数列は、等比数列と周期的な数列の積で表されます。周期が6と考えて解くこともできますが、これを絶対値1、偏角π/6の複素数の実部と考えて、複素数平面を利用することがうまいアイデアです。しかし、類題経験がないと、なかなかこの発想は難しかったと思われます。初見で気づいた方は、センスがあります。

4⃣は、曲線のある部分の長さを求める問題です。方針に迷うところはなく、計算していくだけです。途中で、1/cosθの積分が出てきますが、これは、同学の2019年の1⃣問2と同じ問題です。同学では、受験生の得点が低いと、短いスパンで同じ趣旨の問題を出題することがよくあります。過去の入試問題の研究をきちんと行っていた方は、難なく解けたことと思います。

5⃣は、三角形ABCについて、BとCは定点でAがある条件を満たしながら動くとき、三角形ABCの垂心の軌跡を求める問題です。前述した通り、今年はこの問題のみ（1）・（2）と誘導があります。（1）では、三角形ABCの外心の座標を求めます。すぐに外心は原点Oと分かった方も多いと思いますが、答えだけでは大きな得点にならない可能性が考えられます。なぜその点が外心なのかをきちんと論証したいところです。角BOCの大きさが2π/3だけではなく、外心が線分BCの垂直二等分線上かつ線分BCの上側にあることも書いておきましょう。（2）で軌跡を求めますが、（1）をヒントとすると、Aが中心Oで半径2の円上の点という事実からパラメータ表示する解法がベターです。ヒントを用いずにA（s，t）としても、そこそこの計算で解けます。

6⃣の問1は、3のn乗から2のn乗を引いたものが素数ならば、nも素数を示す問題です。対偶を考えるか、背理法を用います。いずれにしても、nが素数でなければ、「3のn乗から2のn乗を引いたもの」が因数分解できます。問2は、微分可能な関数がある条件を満たすとき、その関数のグラフで表される曲線の接線で原点を通るものが存在することを示す問題です。平均値の定理とある条件を組み合わせて使います。「ある条件」の使い方は、一度経験しておかないとなかなか思いつくことが難しかったと思われます。

全体としては、1⃣、2⃣、4⃣、5⃣のように、方針に迷うところがないストレートな問題が多く、難しかった昨年に比べて易化しました。高得点も可能なセットだったと思われます。ただし同学は、問題が標準的なものでも、厳密な論証ができていない場合は大きな得点にならないことが分かっています。同学を受験予定の方々は、隙のない答案作成を心掛けるようにしていきましょう。

（4）京都大学（文系）
1⃣は、理系と同様に、問1・問2と二つの問題があります。問1は、2進法に関する計算問題です。2進法のものを10進法にして計算して、その結果を2進法、4進法にするというのは大変なので、2進法のまま計算できるようにしたいです。2の何乗という形で書いて、指数法則を用いて計算しても良いでしょう。問2は、三角形の垂心の位置ベクトルを求める問題です。垂心の定義が分かっていれば問題ないでしょう。

2⃣は、絶対値を含む関数の定積分を求める問題です。ストレートな問題で、計算間違いすることなく、必ず正解したい問題です。

3⃣は、確率の問題です。1からnまでの番号がついたn個の箱があり、全てに赤玉と白玉が1個ずつ入っています。まず番号1の箱から玉を1個取り出し、番号2の箱に入れてよくかき混ぜ、次に番号2の箱から玉を1個取り出し、番号3の箱に入れてよくかき混ぜます。この操作を繰り返し番号n－1の箱から玉を1個取り出し、番号nの箱に入れてよくかき混ぜます。最後に番号nの箱から玉を1個取り出し、番号1の箱に入れ、番号1の箱に赤玉と白玉1個ずつ入っている確率を求めます。この条件は、番号1の箱から取り出す玉と番号nの箱から取り出す玉が同じ色であることに注目して、漸化式を立式する、または、箱kに入っていた玉が最後に取り出される確率の総和を求めても良いでしょう。いずれにしても、最初（箱に玉が2個入っている）と2回目以降（箱に玉が3個入っている）で、状況が違うことを忘れてはいけません。

4⃣は、直方体を対角線が含まれる平面で切断したとき、切断面の面積の最小値を求める問題です。切断面が平行四辺形になることを示し、後は根号の中に注目すると、2次関数の最小値を求めれば良いです。切断面が平行四辺形になることを知っていても、きちんと論証できないと同学では高得点はもらえないでしょう。ベクトルを用いると、単純な計算で証明できます。

5⃣は、整数問題です。pが素数ならば、pの4乗に14を加えた数は素数ではないことを示します。ｐを3で割った余りで場合分けし、pが3の倍数でなければ、pの4乗に14を加えたものが3の倍数と分かり、これは30以上の3の倍数なので素数ではない、と分かります。残りのpが3の倍数の場合は、素数かつ3の倍数は3自身のみですから、具体的に計算すれば素数ではないことが分かります。同学の整数問題において、3で割った余りに注目することは、よく出題されるテーマです。最近では、2018年の3があります（同じ年の理系の2も同じ問題です）。文系でも、受験生の得点が低い問題は、短いスパンで繰り返し問われることが多く、同学の志望者の方は、過去の入試問題の研究がかかせません。

全体として、1、2のように、方針に迷うところのないストレートな問題がありましたので、理系同様、難しかった昨年と比べると易化しました。数学が得意な方は高得点も可能だったと思われ、大きな差がついたのではないでしょうか。理系でも書きましたが、同学では、問題が標準的なときほど、厳密な論証が求められる傾向があります。同学を志望される方々は、隙のない答案を作成できるように練習に励んでください。

（5）大阪大学（理系）
昨年、大幅に易化した同学ですが、今年は一昨年までの難易度に近いハイレベルな問題でした。出題分野を見ると、対数関数を含む不等式や整数問題など大阪大学（理系）の頻出分野ばかりですが、場合の数・確率の出題がありませんでした。

1⃣は、ある放物線上の点Pから、双曲線に2本の接線を引き、その接点のx座標をs、tとします。Pが放物線上を動くとき、t/sの最小値を求める問題です。微分の計算はやや煩雑ですが、方針に迷うところはなく、完答を目指したい問題です。

2⃣は、空間の4点が同一平面上にあることがテーマの問題です。典型的な問題で、計算量も少ないので、これは落とせません。

3⃣は、（1）・（2）で不等式を示した後、それを用いて数列の極限を求める問題です。（1）は、両辺の差をとって微分します。（2）は、（1）で得た不等式を積分します。ここまでは落とせません。（3）では、まず数列が収束するための必要条件を考えて、pの値を求めます。ただ、ここでも区分求積の利用に気づかなければいけません。さらに、（2）で得た不等式を用いて、はさみうちの原理からqの値を求めます。（2）の結果を単純に当てはめるだけではなく、どのように用いるか適切な考察が必要です。

4⃣は、整数の問題です。与えられた条件が定積分で表されていますので、まず計算し整理してa、b、cの式にします。（1）では、cが3の倍数であることを示しますので、c以外のa、ｂの式を見て因数分解に気づけるかがポイントです。そうすると、2a＋bまたはa＋2bが3の倍数と分かり、このどちらかが3の倍数ならば、もう一方も3の倍数になりますので、証明が完了します。（2）は、2a＋bとa＋2bがともに3の倍数であることとaとbが共に整数であることが同値であることに気づけば、後は典型的な約数の個数を求める計算です。

5⃣は、曲線C上の接線がCの他の1点と接する必要十分条件を求める問題です。（1）で、三角関数を含む方程式の解が存在することを示します。いつも通り、関数のグラフとx軸に平行な直線がちょうど1点だけ共有点を持つことに帰着させます。関数の値域が全ての実数となることの確認を忘れないようにしましょう。（2）では、まずCと2点で接する直線とは、Cの2点での接線を別に考え、それらが一致すると考えます。これを立式すれば、（1）のヒントにも気づくことができるでしょう。「必要十分条件を求めよ」なので、必要条件と十分条件に分けて考え、丁寧に議論することをおすすめします。

全体としては、1⃣、2⃣のように典型的な問題があり、また誰もが解けない難問は見当たらなかったので、難化とまでは言えませんが、昨年よりも難度が上がっていることは確かでしょう。

（6）東京工業大学
全体的に易化傾向である大学入試数学において、非常に高い難度の問題を出題し続けていた同学ですが、昨年は取り組みやすい問題が大半を占め、5のような難問はありましたが全体としては易化しました。今年は、その反動からか、1を除き2以降は全て発想や論証などでそれぞれのポイントがあり簡単にはいかないものばかりで、やや難化しました。

1⃣は、整数問題と不等式を示す問題です。（1）で、正の整数のどの位にも9が現れない数が、k桁の正の整数の中にいくつあるか求めます。（2）では、（1）で求めた数を1桁からk桁まで考え、それらの逆数を全て足し合わせたものが満たす不等式を示す問題です。上からの評価なので、各数を大きくしていきますが、逆数なので分母を小さくすれば良いことになります。この問題では、n桁の数を全て10のn－1乗に置き換えれば解決できますので、易しめの不等式評価の問題です。

2⃣は、楕円と2直線の四つの共有点の成す四角形についての問題です。力ずくでいくと、楕円の議論特有の面倒な計算が必要となるので、できる限り図形的な考察をからめていきましょう。（2）では、直線lとmの傾きが等しいことに注目して、条件はx座標の差が等しいこととなります。（3）では、（2）から2本の直線lとmが原点について対称になることに注意しましょう。ここからは、さまざまな解法が考えられますが、PQとPSが直交することから、直線ｌとmの傾きが0を得ることが実戦的でしょう。問題文に「すべて求めよ」とありますが、1組のみが答えになります。

3⃣は、いわゆる「カタラン数」の中で素数となるもの全てを求める問題です。カタラン数とは、異なる2n個のものからn個選ぶ組合せの総数をn＋1で割って得られる数です。（1）は、ｎとｎ＋１が互いに素となることを用いましょう。（2）は、数学的帰納法を用いた証明です。ここで数列の第ｋ項と第ｋ＋1項の関係を得ますが、これは（3）でも使えますので、覚えておきたいところです。（3）が問題ですが、nが1、2、3、4と順に計算すればn＝2、3が条件を満たすことは分かります。もう少し先まで計算すれば、これ以上は素数にならないのではないかと気づき、その証明を行うことになります。さまざまな方法が考えられますが、（2）や（2）の途中経過で得られたものを有効に活用したいです。

4⃣は、中心が原点Oで半径が1の球面上を動く四つの点についての関数の問題です。4変数に見えますが、（1）が大きなヒントで、a、b、cの三つをまとめて考えることに気づかせてくれます。（2）では、三つの和の大きさについての関数と考え、最大値が求まります。（3）では、CとDを具体的に定めて、最大値を取るAとBの組として考えられるものを「すべて」求めます。a＋ｂの絶対値の値はaの絶対値とbの絶対値の和以下となる（三角不等式）ということは、常に頭においておきましょう。今はこれらが等しくなり、aとbが決定します。この問題も「すべて」とありますが、答えは一つのみです。

5⃣は、（1）・（2）で円が、境界が曲線である領域に含まれる条件を求め、（3）では（2）で求めた領域をy軸の周りに1回転してできる立体の体積を求めます。曲線と曲線が接する場合は注意が必要で、連立してできた方程式が重解を持つということは、消去した文字によっては成り立たないことがあります。円がこれらの領域に含まれる条件は、円の中心から領域の境界までの距離が半径以上と考えるのが基本です。（3）は、場合分けがありますが、回転体の体積を求める計算は難しくはありません。

全体としては、数学Ⅲの微積分が5の最後だけということが、同学としては大変珍しく（なかったわけではありませんが）、虚をつかれた受験生も多かったのではないでしょうか。また、180分と長い試験時間ですが、問題のボリュームがたっぷりで受験生としては時間が足りないと感じたと思われます。

（7）一橋大学
かつて文系の大学ながらも、高水準な問題を出題していた同学ですが、昨年は典型的といえる問題が大半を占め易化しました。今年は、1が整数で、ラストの5⃣が確率という定番の並びに変化はありませんが、難易度はさらに易化しました。この程度の難易度の方が、適度に差がつき、数学が得意な受験生にとっては有利に働くのかもしれません。

1⃣は、整数問題です。問題文をそのまま引用しますと、「1,000以下の素数は250個以下であることを示せ」です。難しい問題ではありませんが、典型的なものとは言い難いので、戸惑った受験生も多くいたと思われます。実際、1,000以下の素数は168個ありますが、それを全て書き上げても正解ではありません。その他に素数がないことが示されていないからです。そこで、素数ではない数が、1,000以下に750個以上あることを示すことになります。2、3、5の倍数のうち、2、3、5を除いたものを数えると、731個になりますので、残り19個素数ではないものを見つければ終わりです。

2⃣は、数列の和を求める問題です。数列の第k項の中に√kの整数部分が入っているので、そのままでは計算できません。√kの整数部分がmとなるkの個数をmで表してから計算します。

3⃣は、まず（1）で、係数にa、bを含む2次方程式の2解と1の三つを3辺の長さとする三角形の存在条件を考えます。（2）では、（1）をもとに2変数a、bの関数の取り得る値の範囲を求めます。a、ｂの関数がkという値を取るa、bが存在するという条件を満たすkの範囲を求めます。

4⃣は、放物線と円の共通接線、放物線、そしてy軸で囲まれた部分の面積の最大値を求める問題です。数学Ⅲの微積分を知っていると、計算が大幅に簡略化されます。一橋大学を受験予定の方は、計算のみで構わないので、数学Ⅲの微積分まで勉強すると良いでしょう。

5⃣は、確率の問題です。与えられた条件が定積分で表されているので、まずここの計算を行いますが、バラバラにすることなく、ある程度かたまりを意識して計算しましょう。そうすると、掛けて－3になる整数を求める問題になり、4組を個別に考えていきます。

（8）東京医科歯科大学（医学部医学科）
かつては難問が出題されていましたが、昨年、一昨年と標準的な問題が並びました。今年もこの流れが引き継がれており、誰もが手を出しかねる問題は見当たりませんでした。

1⃣は確率の問題ですが、場合の数を数え上げるところがポイントとなります。aから置き換えでbを作り、bから四捨五入してcを作ります。後は方程式や不等式を満たす組を数え上げていきます。後半はやや煩雑になりますが、置き換えなどの工夫を行い、確実に正解したい問題です。

2⃣は、与えられた四角錐に内接する球やその四角錐に含まれる直方体の体積の最大値を求める問題です。最大値を求めるときの計算は、根号の中だけ考えることにより、数学Ⅱの微分で求めることができ、計算は大変ではありません。（3）では、四角錐の底面に一つの面が含まれる直方体の体積が最大となる場合を考えますが、底面に含まれる面と平行な面の四つの頂点が四角錐の辺上にある場合となります。ここの論証は正確さが求められます。

3⃣は、双曲線の問題です。円ではよく見かける問題ですし、双曲線でもよくある問題です。しかし、問題文の表現が固く、戸惑った受験生もいるのではないでしょうか。例えば（2）では、「座標平面上の点で、その点から双曲線に2本の接線を引くことができる点全体を図示せよ」の方がよく見かけるものに近いでしょう。

総じて、数学Ⅲの微積分が全く出題されなかったことは、大変珍しいです。1⃣の確率や2⃣の空間図形は、同学での頻出分野ですが、以前のものと比べると計算量も多くなく、高得点が狙えるセットといえます。

（9）早稲田大学
基幹理工・創造理工・先進理工学部について、一昨年、昨年と標準的な問題が並ぶセットでしたが、今年も全体的な難易度は同じでした。ただし、数学Ⅲの微積分が1⃣の（3）のみで、これは大変珍しいことです。3⃣は複素数平面の問題です。ちなみに同学は昨年度の入試問題の中で「複素平面」という言葉を用いていましたが、今年度は高校の教科書で用いられている「複素数平面」という言葉が使用されています。この問題は、三角形の周または内部を動く点を2乗すると、どのような図形上を動くかを求めます。三角形の周のみを考えても、2乗が表す図形の形状は分かりますが、三角形の内部がどのようにうつるかきちんと議論するところが難しいです。結局、放物線と直線で囲まれる図形になり、最後にその面積を求めます。典型的なx軸についての積分ではなく、y軸についての積分を考えると計算が楽になります。4の確率は、シンプルな設定に見えますが、後半は箱の個数による場合分けが必要になります。箱の個数が2個以上、3個以上という設定のときに、勝手に多くの箱を考えず、2個のとき、3個のときにもどうなるかきちんと考え、隙のない論証を行わなければいけません。

教育学部も、理工学部と同様に、一昨年易化し、昨年はその難易度が踏襲されました。今年は、さらに易化した印象です。また数学Ⅲからの出題が大幅に減少しました。昨年は2⃣以降の大問は全て数学Ⅲからの出題でしたが、今年は1題もありませんでした。2⃣は、三角形の垂心の位置ベクトルを求める問題ですが、（1）の場合分けが煩雑で完全な論証をすることは、なかなか難しかったと思われます。

商学部は、相変わらず取り組みにくい問題が並んでいます。1⃣の小問集合ですら、典型問題は皆無です。3⃣の整数問題は、（1）は正の約数の個数を求める典型問題ですが、（2）の正の約数の和が奇数という条件には、戸惑った受験生も多くいたと思われます。

（10）慶應義塾大学
理工学部は、1⃣が小問集合ではなくなり、大問5題の出題です。一昨年からの易化傾向は継続しており、手を出しかねる難問は見当たりません。しかし、平易な問題も見当たらないので、そう簡単にはいきません。特に今年は昨年と比べて、計算量は増加しています。同学を志望する方々は、こういった問題に取り組み、しっかりとした計算力を身につけることが必要です。2⃣の（2）は、2021次の多項式をある多項式で割った余りを求める問題です。x＋1の3乗を同じ多項式で割った余りが1であることを見抜くことが必要でした。早稲田大学（理工）の2⃣でも、xの2021乗をある多項式で割ったときの余りを求める問題が出題されています。3⃣は、さいころを繰り返し振り、2ｎ＋1回振るか、5以上の目が2回連続して出た場合に終了する実験についての確率の問題です。「5以上の目が2回連続」はよく見ますが、2ｎ＋1回振り終えると終了というルールにより、いろいろと制約が出てきます。その場での理解力が試される良問です。最後の計算も、等比数列と等差数列の積で表される数列によってできる級数の和を求めることになり、気が抜けません。

医学部は、近年易化傾向が続いていましたが、今年はやや難化した印象です。2⃣は長らく漸化式を用いて確率を求める問題でしたが、今年はなんと「データの分析」からの出題でした。「データの分析」は2017年に小問の一つとして出題がありましたが、大問での出題は驚きです。（2）の論証がやや難しい問題であり、共分散が0にならないことを示します。一例としては、共分散が、約分できず整数にならない部分と整数の部分に分かれることを示すことにより、結論を得ます。（4）は、相関係数の最大値と最小値なので、それぞれ1と－1と想像できますが、厳密に考えるには、経験がないと難しかったと思われます。1からnまでの正の整数を並び替えたものが2組あるとし、それらをa（1）、a（2）、…、a（n）とb（1）、b（2）、…、b（n）とするとき、a（1）b（1）＋a（2）b（2）＋…＋a（n）b（n）の最大値と最小値を考えてみてください。

経済学部は、ハイレベルな出題が維持されています。5⃣は単純なベクトルの問題に見えますが、後半は初等幾何の考察が必要な良問です。一方6⃣は、問題に表れるαとβは途中まで関係がありますが、最後の最後にαとβが独立に動くと考えなければならず、奇妙な問題といえます。

商学部は、ついに易化しました。1⃣の小問集合も2問のみで（昨年の1⃣は5問ありました）、70分という試験時間を考えると、これぐらいが適切にも思えます。2⃣以降も確率、微積分、ベクトル、数列という頻出分野からの出題でした。ただし、どの問題も作業量は多く、素早く処理していく力は相変わらず必要といえます。

この記事は『2021年度大学入試 出題傾向リサーチ』に掲載された記事の一部を修正・加筆したWeb版です。

▼『2021年度大学入試出題傾向リサーチ』配布中！
今回ご紹介した各大学の個別試験のほか、大学入学共通テスト、東大、京大、国公立大医学部入試の動向・出題分析を掲載しています。
ご要望の方はこちらからお申し込みください。

▼東大・京大・医学部研究室
SAPIX YOZEMI GROUPが運営する東大・京大・医学部合格を目指す受験生のための総合情報サイトです。入試対策やイベント情報、現役大学生からのメッセージなど、さまざまな情報を発信します。
URL: https://juken.y-sapix.com/