皆さん、こんにちは。

Y-SAPIX数学科では、高校数学の各単元を初めて学んでいる高校生を対象に、「お役立ちシリーズ」の記事を発信していきます。各単元の内容は互いに結び付いており、また難関大と言われる大学の出題ほど、単元横断的な理解が問われます。

お役立ちシリーズ vol.2のテーマは、数学Ⅱの「図形と方程式」です。「図形」と「方程式」という、一見すると関係なさそうな2つが強く結び付く、重要な単元です。この単元をマスターすると、図形を「数式処理」によって扱うことができます。本記事を通じて、学習のポイントを確認していきましょう。

〇「曲線y=f(x)」の捉え方

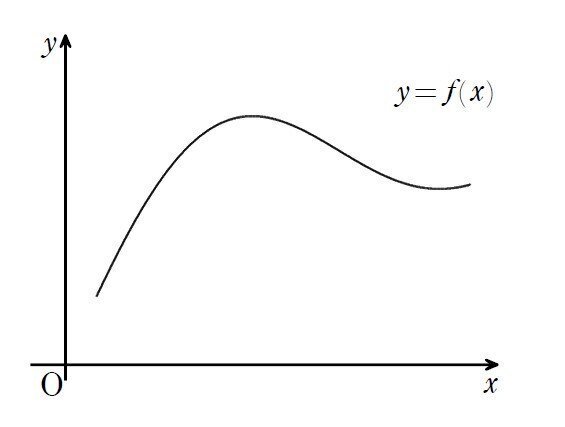
当たり前(？)のことを尋ねるようですが、「曲線$${y=f(x)}$$」とは何でしょうか。例えば、次の図を指差して「この線と近くの数式は、何の関係があるんですか？」と質問されたとき、どう答えますか。(できれば、2通りの説明を考えてみましょう)

説明1
実数$${x}$$を与えたときに、一定のルール$${f}$$によって計算された実数$${f(x)}$$を縦方向に次々とプロットしたのが、曲線$${y=f(x)}$$である。つまり、「原因$${x}$$に対する結果$${f(x)}$$の対応表」である。

説明2
等式「$${y=f(x)}$$」を満たす実数の組$${(x，y)}$$を、点として座標平面にプロットして得られるのが、曲線$${y=f(x)}$$である。つまり、「条件$${y=f(x)}$$で制約された点$${(x，y)}$$の集まり」である。

説明1の捉え方は、最大・最小を考えたり、不等式を解いたりする際に有効です。

一方で説明2は、直線$${y=2x+1}$$には点$${(1，3)}$$のような、等式「$${y=2x+1}$$」を満たす実数の組$${(x，y)=(1，3)}$$に対応する点だけが乗っていることを考えれば納得できるでしょう。そして、「図形と方程式」の根底にあるのは、特に説明2のような曲線の捉え方です。

〇「名前を付ける」ということ

前の見出しでは
　実数$${x，y}$$の条件を与える
→ 点$${(x，y)}$$が制約される
→ $${xy}$$平面の上に図形が現れる
という流れで説明しましたが、実は「図形と方程式」の革命的な点は、むしろ逆の見方にあると言えます。すなわち

　図形を$${xy}$$平面の上に置く
→図形に「名前」$${(x，yの関係式)}$$が付く

という「命名」の見方です。次の図でイメージを掴んでみてください。

言うなれば、「図形と方程式」という単元は

複数の図形が結びつく幾何の世界
(扱うために、発想力が重要)

を丸ごと$${xy}$$平面の上に置くことによって

複数の関係式が結びつく代数の世界
(扱うために、高い発想力は不要)

へ言い換えてしまおう、という単元なのです。

そうして、「代数の世界」での計算結果を今度は「幾何の世界」へとフィードバックすれば、元々の図形についても「よく分かった」となるわけです。

〇式を運用するために

もっとも、「図形の問題」を「計算の問題」へと言い換えたからには、数式を適切に運ぶ技術が求められます。(「発想」の比重が減った分、「計算」の比重が増えた、と考えてください)

この技術とは、具体的には

①数値のミスなく正確に計算する力
②数学的に等価な、より単純な形の情報へと書き換える
　同値変形の力
の2つからなります。

①はともかく、②はある程度の訓練が必要となってくるところです。例えば、放物線の軸に中心を置きながら上下に動く円を考察するために、文字定数$${a}$$ごとに定まる$${x，y}$$の連立方程式

$$
\begin{dcases}{y}={x^2}\\{x^2}+({y-a})^2=1\end{dcases}
$$

の実数解を考察することがありますが、このような場面では同値変形を活用できると、解の構造がかなり見えやすくなります。一方で、同値変形の運び方は学校の授業ではあまり習わないのが実情です。こちらについては、一歩先を目指す高校生のための記事「深掘りシリーズ」で詳しく紹介していく予定です。

それでは、次回の「お役立ちシリーズ」でお会いしましょう！