
数学こぼれ話#10 お役立ちシリーズvol.5 ~相関係数を徹底理解~
今回の記事では「相関係数」について、ひとまわり深い理解を目指してみましょう。数学Iでデータの分析を習ったばかりの高1生から共通テストを控える受験生まで、必見です!
〇複雑な式にも「意味」がある
散布図の中に$${n}$$組の測定値($${x_1}$$,$${y_1}$$), …, ($${x_n}$$,$${y_n}$$)があるとき、
相関係数$${r_{xy}}$$は
$${r_{xy}}$$=$${\dfrac{(x_1-\bar{x})(y_1-\bar{y})+…+(x_n-\bar{x})(y_n-\bar{y})}{\sqrt{\smash[b]{(x_1-\bar{x})^2+…+(x_n-\bar{x})^2}}\sqrt{\smash[b]{(y_1-\bar{y})^2} +…+(y_n-\bar{y})^2}}}$$
($${\bar{x}}$$,$${\bar{y}}$$は平均を表す)
で定義されますが、皆さんはこの式をどのくらい「納得」できていますか? 誰かに式の意味を説明するつもりで、少し考えてみてください。
結論から言うと、$${r_{xy}}$$をこの計算で求めることには2つの理由があります。せっかくなので、その理由を完璧に理解してしまいましょう!
〇準備1 (共分散) ~符号を与える~
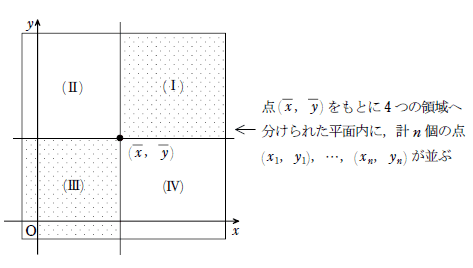
上の散布図を見てみましょう。見やすさのために、点は打っていません。
さて、「正の相関がある」($${x}$$が大きいと$${y}$$も大きい傾向にある)というのは「領域(Ⅰ)(Ⅲ)に入っている点の方が多い」
一方、「負の相関がある」($${x}$$が大きいと$${y}$$は小さい傾向にある)というのは「領域(Ⅱ)(Ⅳ)に入っている点の方が多い」
と言い換えられることが分かります。
このあたりの「多い/少ない」を「プラス/マイナス」で対応させるには、共分散$${s_{xy}}$$
$${s_{xy}}$$=$${\dfrac{(x_1-\bar{x})(y_1-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y})}{n}}$$
を定めると便利です。
$${s_{xy}}$$の分子で足されるのは、ほとんどがプラスとマイナスの数です。
「点($${x_k, y_k}$$)が領域(Ⅰ)(Ⅲ)に含まれる」ということは、式の上では
$${ \begin{cases} x_k-\bar{x}\gt 0 \\ y_k -\bar{y} \gt 0\end{cases}}$$または$${ \begin{cases}x_k- \bar{x}\text{\textless}0\\y_k -\bar{y} \text{\textless}0\end{cases}}$$$${\iff }$$ $${(x_k-\bar{x})(y_k-\bar{y})\gt0}$$
と言い換えられるので、「$${s_{xy} \gt 0}$$」は
$${(x_1-\bar{x})(y_1-\bar{y}),…,(x_n-\bar{x})(y_n-\bar{y})}$$のうち、プラスのものはマイナスのものより多い
つまり
領域(Ⅰ)(Ⅲ)に含まれる点は、領域(Ⅱ)(Ⅳ)に含まれる点より多い
更に
$${n}$$個の点は、概ね左下から右上に並んでいる(正の相関)
と言い換えられます。
なお、点$${(\bar{x},\bar{y})}$$から大きく離れている点$${(x_k,y_k)}$$は「外れ値」として除くのが普通なので、個数のバランスが崩れてしまう$${(x_k-\bar{x})(y_k-\bar{y})}$$は、無いものとして問題ありません。
〇準備2 (内積の不等式) ~意味のある数値を与える~
さて、相関係数$${r_{xy}}$$を
$${r_{xy}=\dfrac{s_{xy}}{s_x・s_y}}$$
と書いたときの分子に来る共分散$${s_{xy}}$$について、よく理解できたと思います。しかし、共分散$${s_{xy}}$$だけでは、2つの散布図における相関の強さを比べることができません。例えば
「数学と英語のテストでは、得点の共分散が4」
「数学と理科のテストでは、得点の共分散が8」
と求まっても、「数学と英語」の相関の強さと、「数学と理科」の相関の強さを単純に比べることはできないのです。
少し発展的ですが、最後の仕上げとして、相関係数の値を-1$${\leqq}$$$${r_{xy}\leqq1}$$に収めるための工夫を見てみましょう。数学Bの「ベクトル」を学習済みの方は、是非読んでみてください。
一般に、$${\overrightarrow{0}}$$でない2つのベクトル$${\overrightarrow{a}}$$,$${\overrightarrow{b}}$$の間には
$${-1\leqq\dfrac{\overrightarrow{a}・\overrightarrow{b}}{\left| \overrightarrow{a} \right| \left| \overrightarrow{b} \right|}\leqq1}$$
(等号成立は$${\overrightarrow{a}}$$//$${\overrightarrow{b}}$$のとき)
という不等式が成り立ちます。いま、$${n}$$次元空間(正確には$${\mathbb{R}^n}$$)のベクトル$${\overrightarrow{a}}$$,$${\overrightarrow{b}}$$として
$${\overrightarrow{a}}$$=$${\begin{pmatrix}x_1- \bar{x}\\ \vdots \\x_n- \bar{x} \end{pmatrix}}$$,$${\overrightarrow{b}}$$=$${\begin{pmatrix}y_1- \bar{y}\\ \vdots \\y_n- \bar{y} \end{pmatrix}}$$
をとれば,先ほどの不等式は
$${-1≦\dfrac{(x_1-\bar{x})(y_1-\bar{y})+…+(x_n-\bar{x})(y_n-\bar{y})}{\sqrt{\smash[b]{(x_1-\bar{x})^2+…+(x_n-\bar{x})^2}}\sqrt{\smash[b]{(y_1-\bar{y})^2} +…+(y_n-\bar{y})^2}}≦1}$$
となり,$${-1≦r_{xy}≦1}$$が成り立つことが分かります。
$${r_{xy}=1}$$(最も強い正の相関)や$${r_{xy}=-1}$$(最も強い負の相関)となるのは
$${n}$$個の点$${(x_1,y_1),…,(x_n,y_n)}$$が点$${(\bar{x},\bar{y})}$$を通る直線上に並ぶとき
ですが、これは「2つのベクトル$${\overrightarrow{a}}$$,$${\overrightarrow{b}}$$の平行」から、直感的にも分かると思います。
さて、ここまで読んだうえで改めて最初の式を見てみると、相関係数$${r_{xy}}$$がこのような式で定義されることを「自然だし、当たり前」と感じられると思います。
統計で登場する数式は難しそうな見た目をしていることが多く、やみくもに覚えようとしても大変です。
しかし、「何を表現したい量なのか」を軸に少し深く学んでみると、案外「自然だし、当たり前」と思えることに気付きます。
それでは、次回の記事でお会いしましょう!

