
数学こぼれ話#9/お役立ちシリーズvol.4~「三角関数」の急所~
お役立ちシリーズvol.4のテーマは「三角関数」です。多くの公式が登場するので、混乱しがちな単元です。本記事を通じて、ポイントを押さえていきましょう。
〇θについて
まず単位円を用意し、$${θ}$$を与えることで$${sinθ}$$,$${cosθ}$$,$${tanθ}$$の値が決まっていきます。この辺りは三角比と同様ですが、三角比では「度数法($${°}$$)」を使ったのに対し、三角関数では「弧度法($${rad}$$)」を使うのが一般的です。以下、$${θ}$$は全て弧度法で表されているとします。さて、$${θ}$$という量は単位円のどこに現れるでしょうか? 頭の中に単位円をイメージして、「ここだ!」と思ったら画面をスクロールして確認しましょう。
↓↓イメージできましたか?下部で確認してみましょう!
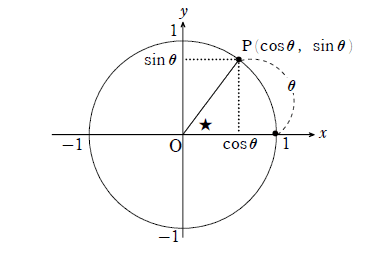
いかがでしょうか? 授業で聞くと、★を指差してくれる方が非常に多いところですが、実は間違いです! 三角関数を真に理解するためには「$${θ}$$は弧の長さである」ということを押さえる必要があります。正確には「$${θ}$$>$${0}$$で反時計回り、$${θ}$$<$${0}$$で時計回り」とする符号付き長さですが、十分に長い巻き尺をイメージすると分かりやすいと思います。
〇周期について
$${sin}$$,$${cos}$$,$${tan}$$は単位円上を動き回る点で定まる値なので、三角関数は周期的な値のとり方をすることが多いです。このような事情から、例えば$${sinθ}$$のグラフは周期が$${2π}$$の波となります。ところで、$${sin2θ}$$の周期が$${4π}$$でなく$${π}$$なのは、パッと分かりますか?
このことは、「$${θ}$$を与える立場」に立つと理解しやすくなります。例えば、$${sinθ}$$は$${\dfrac{π}{2}}$$を与えると$${1}$$になります。
一方、$${sin2θ}$$は
$${θ}$$を与える → $${2倍}$$されて$${2θ}$$になる → $${sin2θ}$$が定まる
という流れで値が定まります。中央のステップで値が必ず$${2}$$倍されるので、同じ「$${1}$$」という値を今度は$${sin2θ}$$にとらせるには、$${\dfrac{π}{4}}$$という半分の値で間に合います。次のグラフを見ながら考えてみましょう。
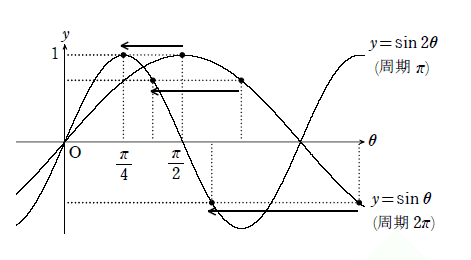
まとめると
「半分の地点」で同じことが起こる → グラフの周期が「半分」になる
ということです。同じように考えれば、$${sin(\dfrac{θ}{2})}$$の周期が$${4π}$$になることも納得できると思います。
〇公式との付き合い方
三角関数で新しく登場する公式のほとんどは、加法定理
$${sin(α±β)=sinαcosβ±cosαsinβ}$$
$${cos(α±β)=cosαcosβ∓sinαsinβ}$$
$${tan(α±β)=\dfrac{tanα±tanβ}{1∓tanαtanβ}}$$ (いずれも複号同順)
が出発点なので、加法定理は確実に押さえましょう。
また、$${2}$$倍角の公式
$${sin2θ=2sinθcosθ}$$
$${cos2θ=\gdef\bar#1{#1^2} \bar{cos}θ-\gdef\bar#1{#1^2} \bar{sin}θ}$$
$${=2\gdef\bar#1{#1^2} \bar{cos}θ-1}$$
$${=1-2\gdef\bar#1{#1^2} \bar{sin}θ}$$
$${tan2θ=\dfrac{2tanθ}{1-\gdef\bar#1{#1^2} \bar{tan}θ}}$$
は加法定理からすぐに導けますが、単純に使用頻度が高いことと、後は「$${2}$$倍角の公式を覚えているから思いつく式変形」があることを考えれば、やはり押さえるべきでしょう。極端な話、他の公式は(導き方さえ分かっていれば、)無理に覚える必要はありません。
公式とは少し違いますが、三角関数の合成もさらっと出来るとよいですね。復習すると、合成は次のような発想で行われるのでした。
$${[\sqrt{\smash[b]{3}}sinθ+1cosθ}$$を$${sin}$$だけで表したい$${]}$$
$${①2(=\sqrt{\smash[b]{\gdef\bar#1{#1^2} \bar{(\sqrt{\smash[b]{3}})}+\gdef\bar#1{#1^2} \bar{1}}})}$$で全体で括る
$${②\sqrt{\smash[b]{3}}sinθ+1cosθ=2(sinθ・\dfrac{\sqrt{\smash[b]{3}}}{2}+cosθ・\dfrac{1}{2})}$$
※( )の部分が「$${sin}$$の加法定理」に似ている
$${=2(sinθcos\dfrac{π}{6}+cosθsin\dfrac{π}{6})}$$
$${=2sin(θ+\dfrac{π}{6})}$$
「$${2}$$で括って加法定理でまとめる」ことだけ押さえておけば、細かいことを何も覚えなくてよいことに気が付きましたか? 一見すると覚えることが多そうな単元ほど、このような「勘どころを掴む」という意識を持って学習すると急に見通しが良くなることが多いです。
さて、三角関数を深く理解するためのポイントを色々と紹介してきましたが、今回はこれくらいにしておきたいと思います。皆さんが学習している三角関数は高校で習って終わりではなく、理工系を始めとする様々な分野の道具として活躍しつづけます。是非、今のうちから使いこなせるようになっておきたいものですね。
それでは、次回の「お役立ちシリーズ」でお会いしましょう!

