
数学と仕事シリーズ#3「ネットワーク効果は二次関数的に増加する」
このシリーズでは、中高生の皆さんが勉強している数学の知識が、ビジネスの世界でどのように使われているかを紹介します。
数学って、将来必要なの?
と思っている皆さんにぜひ読んでほしいと思います。
ネットワーク効果とは
今回はネットワーク効果のお話です。
ネットワーク効果とは、ある個人の言動が他の個人に影響を与えることを言います。
ネットワーク効果が発生するためには、2人以上の集団が存在している必要があります。そして、その集団内で起きる1対1の関係をリンクと呼びます。
【図表A】のように、3人いればリンク数は3、4人いればリンク数は6、5人いればリンク数は10となります。場合の数ですね。
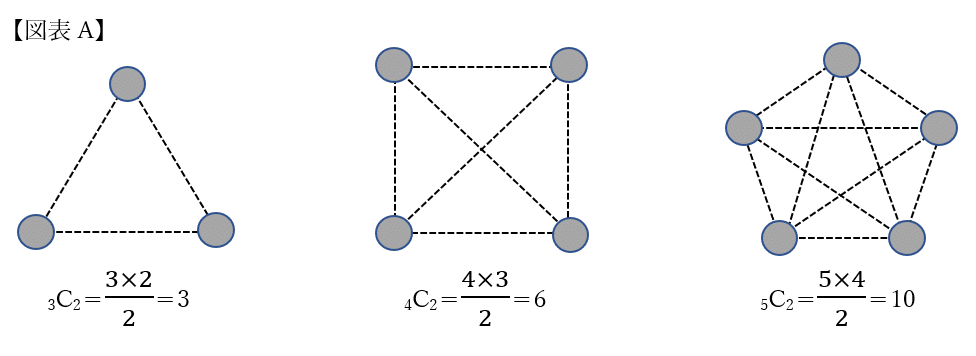
これがネットワーク効果を測定する基本的な考え方です。
皆さんはLINEを使っていますか?
現在、LINEの利用者は9400万人ほどだそうです。
さてこの場合のリンク数はいかほどでしょうか?
普通の電卓ではエラーが出てしまうほどのケタ数になります。
でもちょっと待ってください。
その大きな数に何の意味があるのでしょうか。
(だって、9400万人がみんな知り合いで、しかも仲良しでおしゃべりしたり、お出かけしたりするわけではないですよね。)
現実的には算出されたリンクがすべて生じることはありません。
でもいいのです。
ネットワーク効果はリンクが発生する可能性を評価しているわけです。
リンク数は二次関数的に増加する
ネットワーク効果の計算式を一般化してみましょう。
【計算式A】をご覧ください。

リンク数がNの二次関数になっていることが分かります。
ではグラフを描いてみましょう。
頂点の座標および横軸との交点を調べます。
【計算式B】をご覧ください。

グラフを描くと【図表B】のようになります。
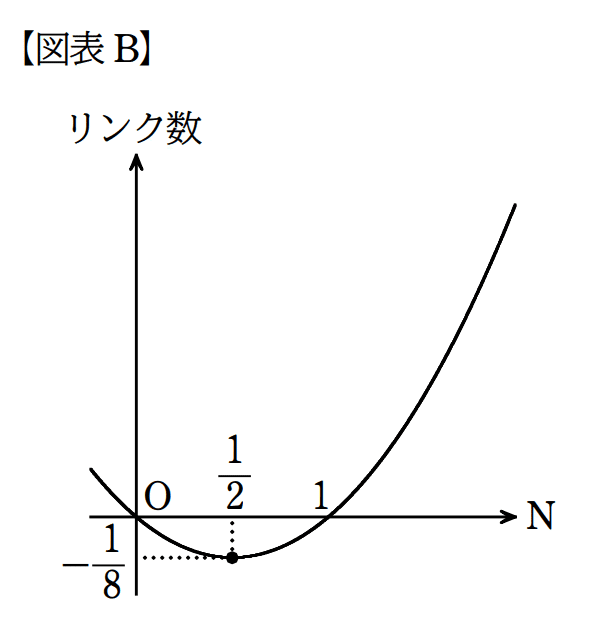
もう一息です。
リンク数がマイナスになったり、グラフが第二象限をずっと伸びていくというのも変な話です。
Nの値に条件がありそうです。
そもそもリンクは2人以上の個人間で生じる関係のことですから、集団内の人数は1を超えていなければいけませんね。
したがって、定義域はN>1です。
改めてグラフを描き直してみると【図表C】のようになります。

リンク数は二次関数的に増加する。
SNS各社がひとりでも多くのユーザーを獲得しようとする理由がよく分かります。
■2023共通テストで的中問題あり!
■大学受験、決めるなら。

