
数学こぼれ話#7/お役立ちシリーズvol.3~放物線の平行移動を攻略~
皆さん、こんにちは。
Y-SAPIX数学科では、高校数学の各単元を初めて学んでいる高校生を対象に、「お役立ちシリーズ」の記事を発信していきます。各単元の内容は互いに結び付いており、また難関大と言われる大学の出題ほど、単元横断的な理解が問われます。
お役立ちシリーズ vol.3のテーマは、数学Ⅰの二次関数で学習する、グラフの平行移動です。放物線であれば軸や頂点に注目すれば平行移動できてしまいますが、本記事では「$${x}$$や$${y}$$に変更を加える」という、より様々なグラフへ応用できる方法について、確認してみましょう。
一歩背伸びして、高校範囲の二次関数を勉強し始めた中学生から質問されたとしましょう。二次関数を学習済みの皆さんなら、どう答えますか?
(問)
放物線 $${y=(x-3)^2}$$は、放物線 $${y=x^2}$$ を$${x}$$ 軸方向に$${3}$$だけ平行移動したものになるのはなぜですか?$${x}$$としていろいろな整数を入れた表を見れば「納得」はできるけれど、もう少ししっかりと「理解」してみたいです。
いかがでしょうか。「表で納得していたのに、どうしようか…。」と思った方もきっと多いと思います。
実は、前回の記事 #6が、この問いに答えるためのヒントになっています。
(数学Ⅱの「図形と方程式」という単元を題材にしていますが、まだ習っていない方も是非読んでみましょう。)
ここでは、放物線$${y=(x-3)^2}$$を
各地点$${x}$$において縦方向に$${y}$$座標として$${(x-3)^2}$$の値をプロットした点の集まり
と捉える、グラフの見方が役立ちます。
次に示す目標と手順を、下にある図と見比べながら読んでみてください。
($${X}$$は実数の定数です。)
目標:地点$${X}$$において縦方向に$${y}$$座標として$${(X-3)^2}$$をプロットしたい。
手順:
① 地点$${X}$$から$${-3}$$進んで地点$${X-3}$$に移動する。
② 地点$${X-3}$$において縦方向に$${y}$$座標として$${(X-3)^2}$$をプロットする。
(※この対応は$${y=x^2}$$の対応と同じです)
③ 地点$${X}$$において縦方向に$${y}$$座標が$${(X-3)^2}$$ である点がプロットされる。
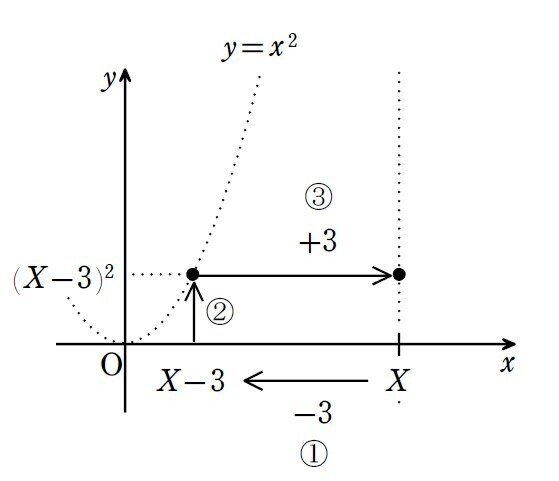
こういうことを、あらゆる実数$${X}$$に対して行なってやると、私達には「放物線が平行移動した!」と見えるわけですね。
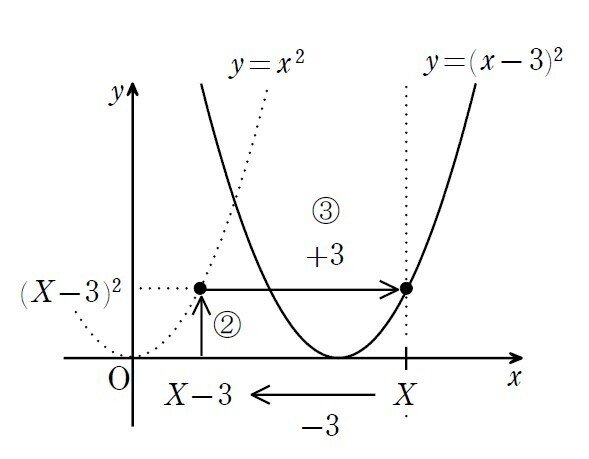
今回は具体的に放物線$${y=(x-3)^2}$$ で考えてみましたが、一般のグラフ $${y=f(x)}$$を$${x}$$軸方向に$${p}$$,$${y}$$軸方向に$${q}$$だけ移動したグラフの式が $${y=f(x-p)+q}$$で与えられることも、全く同じように理解できます。
更に、$${x}$$軸や$${y}$$軸についての対称移動なども、今回確認した方法を応用すれば、同じように理解できますので、是非やってみてください。
それでは、次回の「お役立ちシリーズ」でお会いしましょう!

