皆さん、こんにちは。

2023年度の数学こぼれ話は「対話シリーズ」と「実社会シリーズ」の2本柱で進んでいきます。

対話シリーズは、「数学の中で急に出てきて、実は納得できていない…」と感じやすい内容について、対話形式で理解していくシリーズです。

Y-SAPIXが大切にしている「なぜ？」が伝わる記事を、ぜひお楽しみください！

Y太とS子は高校2年生。学校の授業がまもなく「三角関数」に入るので、高1の時に学習した「三角比」を急いで復習中…。

Y太：単位円の使い方を思い出したので、これで何とか大丈夫かな。

S子：私も一通りの問題は解けるようになったみたい。そういえば、「$${\cos\theta}$$の値がマイナスになる」というのが、イマイチしっくり来ていないんだよね。今更だけど。

Y太：最初は「(底辺)÷(斜辺)を$${\cos\theta}$$とします」と教わるよね。直角三角形の長さの比なので、もちろんプラスの値しか出ないはずで…。次に単位円を使って$${\cos\theta}$$を定義しなおした時、確かに「なんで比にこだわらないんだろう？」とは思ったかな。

S子：「思った」ってことは、もうY太の中では解決してるってこと？

Y太：まぁ、自分なりにはね。せっかくだから、考えてみよう。

Y太：まず、直角三角形から始めよう。拡大や縮小をしても、三角比の値は変わらないのは大丈夫？

S子：要するに、図1みたいなことだよね。左側の直角三角形を、斜辺の長さが1となるように縮小しても、$${\cos\theta}$$の値は$${\frac{4}{5}}$$のまま一定で…。

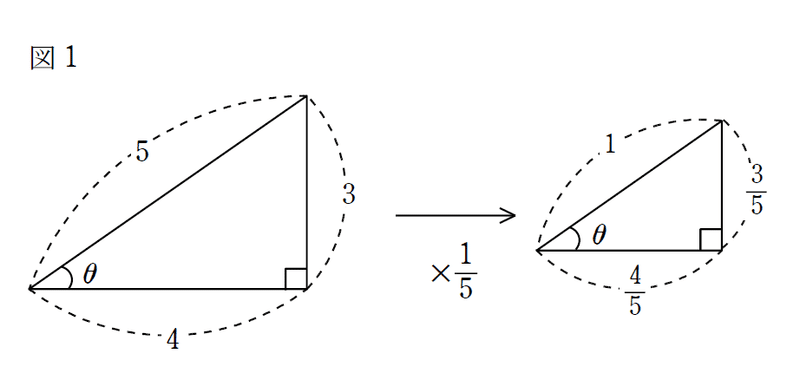
Y太：そうそう。拡大・縮小で$${\theta}$$は変わらないし、何より斜辺を1にしておけば、単位円の中にピッタリはめ込めるからね。(底辺)÷(斜辺)を毎回計算しなくても、埋め込まれた直角三角形の底辺の長さだけ読めば、即座に$${\cos\theta}$$の値が分かる。ちょうど、図2のようになるわけ。だったら、最初から斜辺は1としておいた方が便利だね。

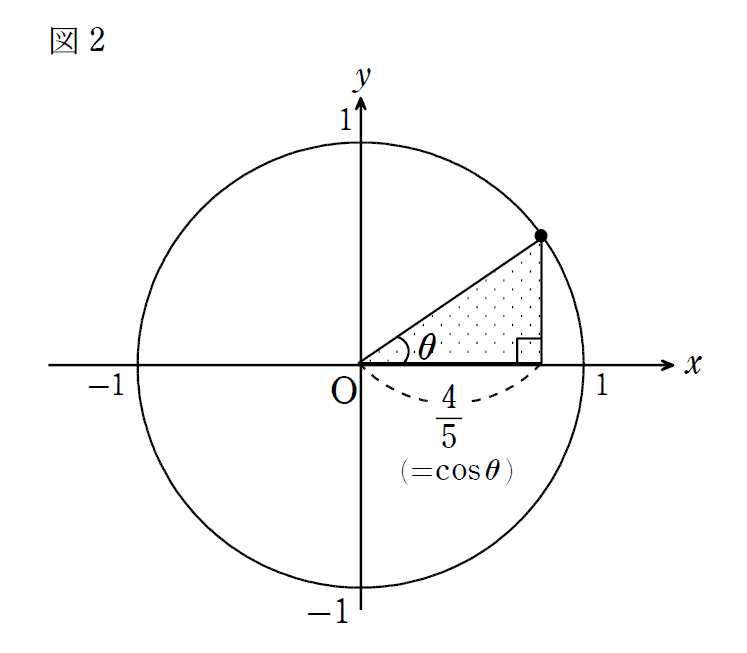
S子：とりあえず、「最初から単位円で考えよう」という気にはなってきたかな。例えば$${\cos60\degree}$$の値が欲しければ、単位円を描いて$${60\degree}$$を測って、直角三角形の底辺の長さを読み取れば、「$${\cos60\degree}$$$${=}$$$${\frac{1}{2}}$$」。　

Y太：そうそう。

S子：…なんだけど、測る角を大きくしていって、例えば$${120\degree}$$で現れる直角三角形の底辺の長さを見て「$${\cos120\degree}$$$${=}$$$${\frac{1}{2}}$$」とはしないのが、唐突だなぁと思ったんだよね。なぜ、「x座標を読み取って$${-\frac{1}{2}}$$」とするんだろう？ 今まで通り、「$${\frac{1}{2}}$$」でいい気がするけど…。

Y太：「定義だから」で済ませてしまえばそれまでだけど、「底辺の長さ」ではなく「$${x}$$座標」の方を採用するなら、それなりの理由があるはず。「$${\cos\theta}$$の定義」なんて天から降ってくるようなものではなくて、人間が決めた約束だからね。ひとつの例として、余弦定理を考えてみよう。

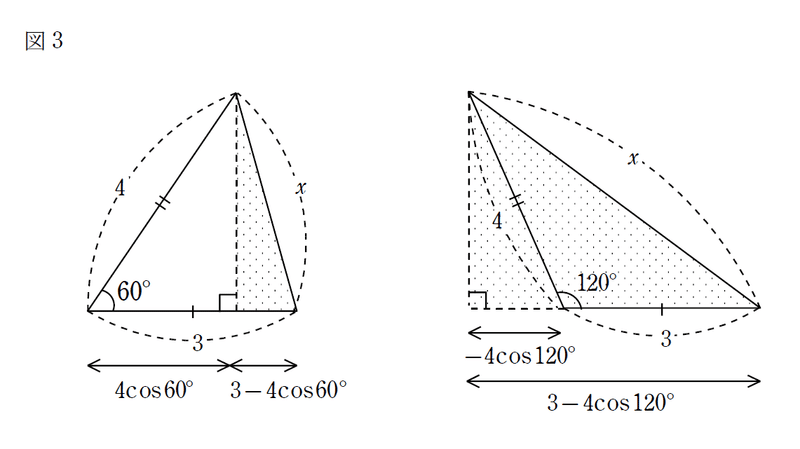
S子：どちらも「余弦定理で一発！」の状況だけど、これがどうしたの？

Y太：余弦定理の証明では、「図3の打点部でそれぞれ三平方の定理を使って$${x}$$を求める」みたいなことをしたはず。詳しい計算は省くけど、長さ3，4で挟まれた角の大きさがどんな場合でも

$${x^2=3^2+4^2-2\cdot3\cdot4\cos\theta}$$

と計算されるには、$${\cos120\degree}$$の値を「$${\frac{1}{2}}$$」ではなく「$${-\frac{1}{2}}$$」とすると都合が良いんだ。

S子：裏を返すと、「比にこだわる」形で$${\cos\theta}$$を定義すると、単なる余弦定理でさえ、$${\theta}$$ごとの場合分けが出てしまって面倒になる…。

Y太：まさにその通り！

S子：うーん、ものすごく納得。それにしてもY太って、こんなに数学が得意だったっけ？なんだか先を越されちゃった感じ。

Y太：実のところ、余弦定理のくだりは前に兄から聞いた内容なんだけどね。それ以外にも「$${\cos}$$の値を0以上に限定してしまうと、基本的な関数『$${\cos{x}}$$』の性質が悪くなってしまう」みたいなことも言っていたけど、こっちの方は正直よく分からなかったな。

S子：お互い、まだまだこれからってことね！

ちなみに、Y太のお兄さんが言っていた話は「$${\left|\cos{x}\right|}$$の微分可能性」と言い直すことができます。数学Ⅲを勉強済みの方は、こちらについても考えてみてください。

それでは、次の「対話シリーズ」で再びお会いしましょう！

■Y-SAPIXで数学を始めよう！

■2023共通テストで的中あり！